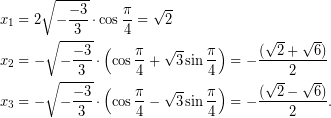Το “χρέος” των μιγαδικών
“[…] Έχετε υπάρξει βετεράνοι των δημιουργικών βασάνων. Συνεχίστε να εργάζεστε με την πίστη ότι τα αναίτια βάσανα είναι λυτρωτικά. […]”
Μάρτιν Λούθερ Κινγκ, “Έχω ένα όνειρο”
Το αδιέξοδο στη μέθοδο για τις εξισώσεις τρίτου βαθμού
Το αδιέξοδο, στο οποίο οδηγήθηκε η μέθοδος των “Καρντάνο – Ταρτάλια”, σχετικά με το πρόβλημα της επίλυσης για τις εξισώσεις τρίτου βαθμού του τύπου,
(1) ![]()
στην περίπτωση όπου,
![]()
σηματοδότησε την υλοποίηση της ιδέας της διεύρυνσης του συνόλου ![]() των πραγματικών στο σύνολο
των πραγματικών στο σύνολο ![]() των μιγαδικών.
των μιγαδικών.
Πλέον, με τη συγκρότηση του ![]() , επανακάμπτει, για την (1), η προσπάθεια αναζήτησης λύσης της μορφής,
, επανακάμπτει, για την (1), η προσπάθεια αναζήτησης λύσης της μορφής, ![]() , όπου,
, όπου, ![]() , τέτοια, ώστε,
, τέτοια, ώστε,
![]()
ή, ισοδύναμα, τέτοια ώστε,
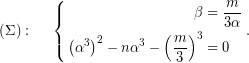
Εξισώσεις τρίτου βαθμού και η διαμόρφωση των μιγαδικών
Είναι αξιοσημείωτο ότι, στο πλαίσιο της αναζήτησης λύσης για το (Σ), ανακύπτουν βασικές έννοιες για το σύνολο ![]() . Για παράδειγμα, οι ορισμοί του συζυγούς, του μέτρου, της τριγωνομετρικής μορφής ενός μιγαδικού αριθμού, καθώς και τα θεμελιώδη συμπεράσματα που τους διέπουν, προκύπτουν με αφορμή την προηγούμενη αναζήτηση.
. Για παράδειγμα, οι ορισμοί του συζυγούς, του μέτρου, της τριγωνομετρικής μορφής ενός μιγαδικού αριθμού, καθώς και τα θεμελιώδη συμπεράσματα που τους διέπουν, προκύπτουν με αφορμή την προηγούμενη αναζήτηση.
Ωστόσο, τίποτα από τα προηγούμενα δε θα θεωρηθεί εκ προοιμίου γνωστό προτού καταλήξουμε στον τύπο λύσεων για τις παραπάνω εξισώσεις τρίτου βαθμού. Απεναντίας, τα δημιουργικά ερωτήματα των προγόνων μας θα αφεθούν να συνοδεύσουν τη διερεύνησή μας. Αυτά θα προικοδοτήσουν το νέο σύνολο οικοδομώντας τα κυριότερα χαρακτηριστικά του.
Παρατήρηση 1 Στο σύνολο ![]() , μια εξίσωση της μορφής,
, μια εξίσωση της μορφής, ![]() με
με ![]() , ισοδύναμα, γράφεται,
, ισοδύναμα, γράφεται,
![]()
επομένως, έχει ακριβώς δύο λύσεις τις ![]() και
και ![]() .
.
Με βάση την προηγούμενη παρατήρηση, από τη δεύτερη εξίσωση του (Σ), έπεται ότι,
![]()
Οπότε, μια δυνατή επιλογή για το ![]() , μπορεί να προκύψει από την ισότητα,
, μπορεί να προκύψει από την ισότητα,
(2) ![]()
ενώ, η αντίστοιχη επιλογή για το ![]() πρέπει να πληροί,
πρέπει να πληροί,
(3) ![]()
Συζυγείς μιγαδικοί
Αν υποτεθεί ότι υπάρχει, για τη (2), λύση της μορφής,
![]()
εύλογα, διερωτάται κανείς, αν, όπως στην περίπτωση όπου ![]() , ο αντίθετος του συζυγή του
, ο αντίθετος του συζυγή του ![]() ,
,
![]()
είναι λύση της (3).
Η απάντηση είναι καταφατική και απορρέει από την ιδιότητα,
![]()
που, εύκολα, αποδεικνύεται ότι ισχύει για οποιουσδήποτε ![]() .
.
Πράγματι,
![]()
Επειδή,
![]()
αρκεί, λόγω του (Σ), να βρεθούν ![]() τέτοια, ώστε,
τέτοια, ώστε,
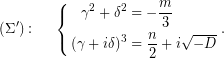
Παρατήρηση 2 Αφού ![]() , προφανώς
, προφανώς ![]() .
.
Η Τριγωνομετρική μορφή
Η πρώτη εξίσωση του (Σ΄), γράφεται,
![Rendered by QuickLaTeX.com \[ \Bigg(\dfrac{\gamma}{\sqrt{-\dfrac{m}{3}}}\Bigg)^2+\Bigg(\dfrac{\delta}{\sqrt{-\dfrac{m}{3}}}\Bigg)^2=1. \]](https://dkonas.sites.sch.gr/wp-content/ql-cache/quicklatex.com-df815b3611b7d9bad2b09a65ec0cbff3_l3.png)
Θέτουμε,
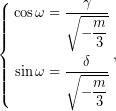
άρα,
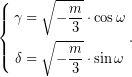
(Με ![]() συμβολίζονται το συνημίτονο και το ημίτονο αντίστοιχα.)
συμβολίζονται το συνημίτονο και το ημίτονο αντίστοιχα.)
Αντικαθιστώντας στη δεύτερη εξίσωση του (Σ΄),
![]()
επομένως,
![Rendered by QuickLaTeX.com \[ \left(\cos\omega+i\sin\omega\right)^3=\dfrac{\dfrac{n}{2}}{\sqrt{-\dfrac{m}{3}}^{3}}+i\dfrac{\sqrt{-D}}{\sqrt{-\dfrac{m}{3}}^{3}}. \]](https://dkonas.sites.sch.gr/wp-content/ql-cache/quicklatex.com-68341300b74068671438601717141516_l3.png)
Το Θεώρημα De Moivre
Με τη βοήθεια γνωστών τριγωνομετρικών ταυτοτήτων,
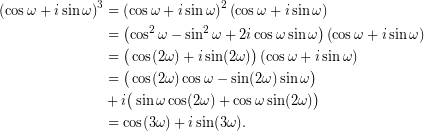
Συνεπώς,
![Rendered by QuickLaTeX.com \[ \cos(3\omega)+i\sin(3\omega)=\dfrac{\dfrac{n}{2}}{\sqrt{-\dfrac{m}{3}}^{3}}+i\dfrac{\sqrt{-D}}{\sqrt{-\dfrac{m}{3}}^{3}}. \]](https://dkonas.sites.sch.gr/wp-content/ql-cache/quicklatex.com-2b8dc8580731b5f3e38c2f12679011c0_l3.png)
Άρα, αρκεί να βρεθεί γωνία ![]() τέτοια, ώστε,
τέτοια, ώστε,
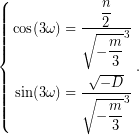
Όμως,
![Rendered by QuickLaTeX.com \[ \Bigg(\dfrac{\dfrac{n}{2}}{\sqrt{-\dfrac{m}{3}}^{3}}\Bigg)^2+\Bigg(\dfrac{\sqrt{-D}}{\sqrt{-\dfrac{m}{3}}^{3}}\Bigg)^2=\dfrac{\Big(\dfrac{n}{2}\Big)^2-D}{-\Big(\dfrac{m}{3}\Big)^3}=1, \]](https://dkonas.sites.sch.gr/wp-content/ql-cache/quicklatex.com-49dd34f417273028e7a607a3ccfdba3c_l3.png)
δηλαδή, υπάρχουν άπειρες λύσεις για το παραπάνω σύστημα.
Η τριγωνομετρική λύση του Viète για τις εξισώσεις τρίτου βαθμού
Αν ![]() είναι μια τέτοια λύση, τότε,
είναι μια τέτοια λύση, τότε, ![]() είναι λύση του (Σ΄), όπου,
είναι λύση του (Σ΄), όπου,
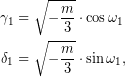
οπότε, ![]() είναι λύση του (Σ), με,
είναι λύση του (Σ), με,
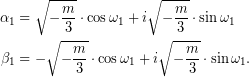
Άρα,
![]()
είναι μία πραγματική λύση της (1).
Με τη βοήθεια αυτής της λύσης, η (1) μετασχηματίζεται ως εξής,
![]()
![]()
![]()
![]()
![]()
![]()
συνεπώς, γράφεται, τελικά,
(4) ![]()
Το τριώνυμο,
![]()
έχει διακρίνουσα,
![]()
Τελικά, η (1), όταν ![]() έχει τρεις πραγματικές λύσεις που δίνονται από τους τύπους,
έχει τρεις πραγματικές λύσεις που δίνονται από τους τύπους,
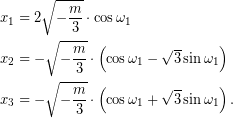
ή, ισοδύναμα,
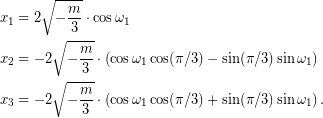
οπότε,
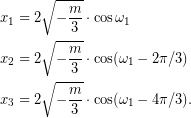
Παράδειγμα 1 Για την εξίσωση, ![]() , έχουμε,
, έχουμε, ![]() , συνεπώς,
, συνεπώς,
![]()
Αναζητείται ![]() , τέτοιο, ώστε,
, τέτοιο, ώστε,
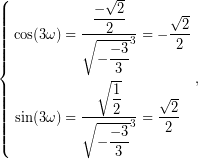
οπότε, μπορεί να επιλεγεί ως ![]() το
το ![]() .
.
Άρα, η εξίσωση έχει τρεις πραγματικές λύσεις,