Η λογαριθμική συνάρτηση

Μοιραστείτε το!

Εισαγωγή

Η λογαριθμική συνάρτηση είναι σήμερα γνωστή, κυρίως, για τις εφαρμογές της σε ένα ευρύ φάσμα πεδίων. Αυτές εκτείνονται από τον αριθμό pH, για την οξύτητα ενός διαλύματος, αλλά και την κλίμακα Richter, για το μέγεθος ενός σεισμού ορισμένης έντασης, ως την κλίμακα του μεγέθους ενός αστέρα, αναφορικά με τη λαμπρότητά του, καθώς και τον νόμο των Webner – Fechner για την ανθρώπινη αντίληψη σ’ ένα φυσικό ερέθισμα.

Στο παρελθόν, περίπου τετρακόσια χρόνια νωρίτερα, η λογαριθμική συνάρτηση είχε συνδεθεί, άρρηκτα, με ένα πρόβλημα προσδιορισμού του εμβαδού ενός καμπυλόγραμμου χωρίου.

Άραγε, υπάρχει κάποια συνάφεια μεταξύ όλων αυτών των φαινομενικά ετερόκλητων εφαρμογών;

Λογάριθμοι

Αρχικά, ας θυμηθούμε την έννοια του λογαρίθμου. Από τον ίδιο τον όρο φαίνεται να υπάρχει κάποια συσχέτιση με τους λόγους και τις αναλογίες.

Τον 17^ο αιώνα, όταν άρχισε να στοιχειοθετείται η έννοια των λογαρίθμων, μια γεωμετρική πρόοδος αναπαριστανόταν ως συνεχής αναλογία. Για παράδειγμα, η παρακάτω ακολουθία λόγων,

$\frac{2}{1}=\frac{4}{2}=\frac{8}{4}=\frac{16}{8}=\frac{32}{16}=\frac{64}{32}=\frac{128}{64}=\frac{256}{128}=\frac{512}{256}=\frac{1024}{512}=\ldots ,$

συμβόλιζε τη γεωμετρική πρόοδο με πρώτο όρο $\alpha_1=1$ και λόγο $\lambda=2$ .

Στην παραπάνω αναλογία, ποιος είναι ο αριθμός των λόγων μέχρι να προκύψει το $32$ ως αριθμητής; Μπορείτε να απαντήσετε στο αντίστοιχο ερώτημα για τον αριθμό $8$ ; Για τους αριθμούς $2$ και $1$ ; Αυτό, που, κάθε φορά, ζητήθηκε, είναι οι λογάριθμοι των αριθμών αυτών με βάση το λόγο της παραπάνω γεωμετρικής προόδου.

Σήμερα, γενικότερα, ο λογάριθμος, $\mathrm{log}_{\alpha}\theta$ , ενός θετικού αριθμού $\theta$ , με βάση $\alpha$ , όπου $0<\alpha\neq1$ , ορίζεται να είναι ο εκθέτης $\kappa$ στον οποίο όταν υψωθεί η βάση $\alpha$ προκύπτει το $\theta$ . Επομένως, ισχύει η ισοδυναμία,

$\mathrm{log}_{\alpha}\theta=\kappa\Leftrightarrow \alpha^\kappa=\theta.$

Για παράδειγμα, $\mathrm{log}_{10}10000=4$ , διότι $10^4=10000$ και $\mathrm{log}_{e}\sqrt{e}=\dfrac{1}{2}$ , αφού $e^{\frac{1}{2}}=\sqrt{e}$ .

Με βάση τον προηγούμενο ορισμό, ένας εκθέτης, σε μια μαθηματική σχέση, θα μπορούσε, υπό προϋποθέσεις, να εκφραστεί ως λογάριθμος με κατάλληλη βάση. Για παράδειγμα, η εξίσωση $10^x=5$ δίνει $x=\mathrm{log}_{10}5$ ή από την ισότητα $\lambda\cdot e^r=\mu$ , έπεται ότι $r=\mathrm{log}_{e}(\frac{\mu}{\lambda})$ .

Ας επικεντρωθούμε, λοιπόν, στο συμπέρασμα ότι ορισμένοι εκθέτες παριστάνονται από λογαρίθμους.

Η λογαριθμική συνάρτηση

Για τη λογαριθμική συνάρτηση, $y=\mathrm{log}_{\alpha}x$ , αξίζει να φωτιστεί μια ιδιαίτερη πτυχή της. Να θεωρήσετε δύο μεγέθη, όπου, καθώς το πρώτο μεταβάλλεται γεωμετρικά (οι τιμές του συγκροτούν γεωμετρική πρόοδο), το δεύτερο μεταβάλλεται αριθμητικά (οι τιμές του συγκροτούν αριθμητική πρόοδο). Τότε, η σχέση που καθορίζει τα δύο μεγέθη είναι λογαριθμική.

Για παράδειγμα, στον παρακάτω πίνακα,

$x$ (γεωμετρική πρόοδος με πρώτο όρο $\alpha_1=1$ και λόγο $\lambda=10$ .)	$1$	$10$	$100$	$1000$
$y$ (αριθμητική πρόοδος με πρώτο όρο $\beta_1=1$ και διαφορά $\omega=1$ .)	$0$	$1$	$2$	$3$

τα στοιχεία της δεύτερης σειράς είναι οι λογάριθμοι, με βάση το $10$ , των αντίστοιχων στοιχείων της πρώτης σειράς. Δηλαδή, $y=\mathrm{log}_{10}x$ . Το συμπέρασμα είναι απόλυτα συνεπές με το πνεύμα των λογαρίθμων όπως αναλύθηκε στην προηγούμενη παράγραφο. Άλλωστε, οι αριθμοί της δεύτερης σειράς είναι οι εκθέτες που αντιστοιχούν στις δυνάμεις, με βάση το $10$ , της πρώτης σειράς.

Αντίστοιχα, για τον πίνακα,

$x$ (γεωμετρική πρόοδος με πρώτο όρο $\alpha_1=2$ και λόγο $\lambda=3$ .)	$2$	$6$	$18$	$54$
$y$ (αριθμητική πρόοδος με πρώτο όρο $\beta_1=5$ και διαφορά $\omega=3$ .)	$5$	$8$	$11$	$14$

ισχύει $y=3\cdot\mathrm{log}_{3}x+5-\mathrm{log}_{3}2$ . Εδώ, η τεκμηρίωση δεν είναι τόσο απλή και αφήνεται ως άσκηση.

Υπάρχουν πολλά παραδείγματα, από την εμπειρία μας, όπου η συμεταβολή δύο μεγεθών συντελείται σύμφωνα με το παραπάνω μοτίβο. Μια ενδεικτική αναφορά έγινε στην εισαγωγή που προηγήθηκε. Στη συνέχεια, θα εστιάσουμε, λόγω της ιστορικής της αξίας για τη Γεωμετρία και την Ανάλυση, στη σύνδεση της λογαριθμικής συνάρτησης με τον υπολογισμό του εμβαδού ενός κατάλληλου επίπεδου χωρίου. Πιο αναλυτικά, θα γίνει μια ερμηνεία της λογαριθμικής συνάρτησης μέσα από το πρίσμα του τετραγωνισμού της υπερβολής.

Τετραγωνισμός χωρίων

Γενικά, για ένα δεδομένο επίπεδο σχήμα, ο τετραγωνισμός του σημαίνει την εύρεση ενός τετραγώνου ισοδύναμου (ισεμβαδικού) με αυτό. Αυτομάτως, κάτι τέτοιο οδηγεί στον υπολογισμό του εμβαδού του επίπεδου σχήματος. Στις περισσότερες περιπτώσεις, αυτό, ακριβώς, εξυπηρετεί ο τετραγωνισμός του. Το (ισοδύναμο) τετράγωνο επιστρατεύεται για να “μετρήσει” το εμβαδό του τετραγωνισμένου χωρίου.

Τα προβλήματα τετραγωνισμών κατέχουν περίοπτη θέση στην ιστορία της Γεωμετρίας. Το πιο διάσημο πρόβλημα τετραγωνισμού, ο τετραγωνισμός του κύκλου με κανόνα και διαβήτη, αποτελούσε τον διακαή πόθο των αρχαίων Ελλήνων και ένα από τα τρία άλυτα προβλήματα της αρχαιότητας. Σπουδαίοι μαθηματικοί, διάφορων εθνικοτήτων και σε διάρκεια εκατοντάδων ετών, καταπιάστηκαν με το πρόβλημα. Αρκετές φορές η μελέτη τους στράφηκε προς την κατεύθυνση του τετραγωνισμού διάφορων άλλων καμπυλόγραμμων χωρίων. Από τον τετραγωνισμό των μηνίσκων του Ιπποκράτη, κατά την αρχαιότητα, ως τον τετραγωνισμό χωρίων που οριοθετούνται, κατάλληλα, από τις καμπύλες της παραβολής και της υπερβολής, κατά τον 17^ο αιώνα, τα πολύ ενδιαφέροντα συμπεράσματα αναπτέρωναν τις ελπίδες για την αντιμετώπιση της περίπτωσης του κύκλου. (Παρεμπιπτόντως, το 1882, αποδείχθηκε το αδύνατο του τετραγωνισμού του κύκλου με κανόνα και διαβήτη.)

Ο τετραγωνισμός της υπερβολής

Μια συγκεκριμένη μέθοδος “τετραγωνισμού” της υπερβολής, $y=\dfrac{\alpha}{x}, \,\,\,\, x \neq 0$ , αναδεικνύει την έννοια της λογαριθμικής συνάρτησης. Όπως θα γίνει αντιληπτό, πρόκειται για μια ατέρμονη διαδικασία, πρόδρομο της θεωρίας της ολοκλήρωσης που διδάσκεται στη Γ΄ Λυκείου. Όσο η άπειρη αυτή διαδικασία επαναλαμβάνεται, σταδιακά, τόσο αποκαλύπτεται η λογαριθμική συνάρτηση με βάση τον αριθμό $e$ του Euler.

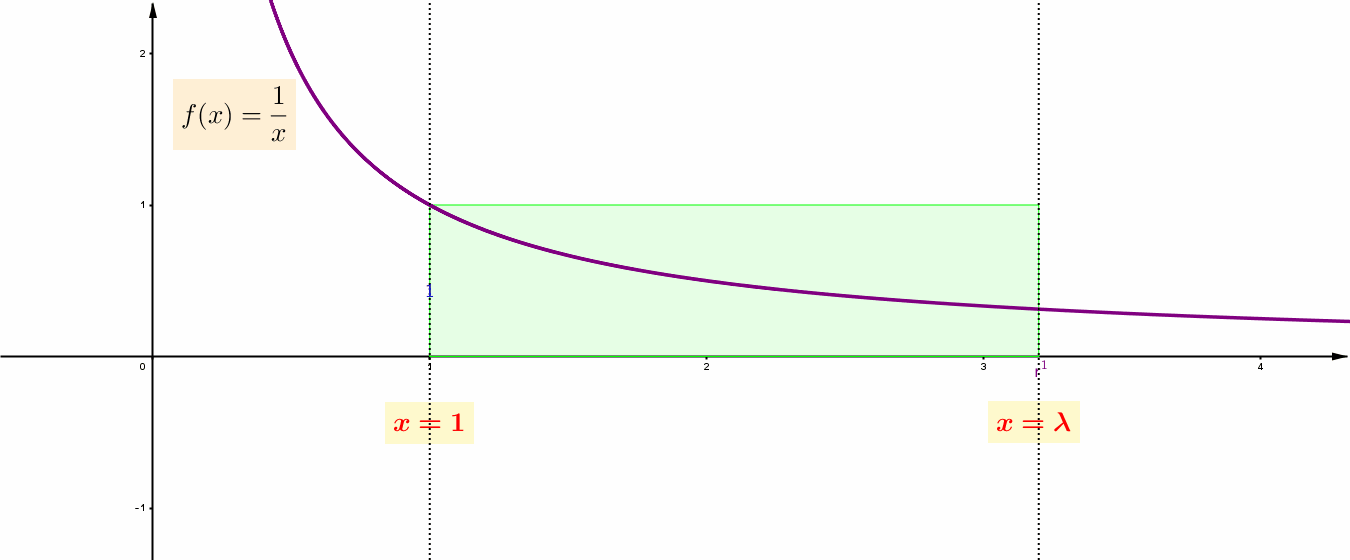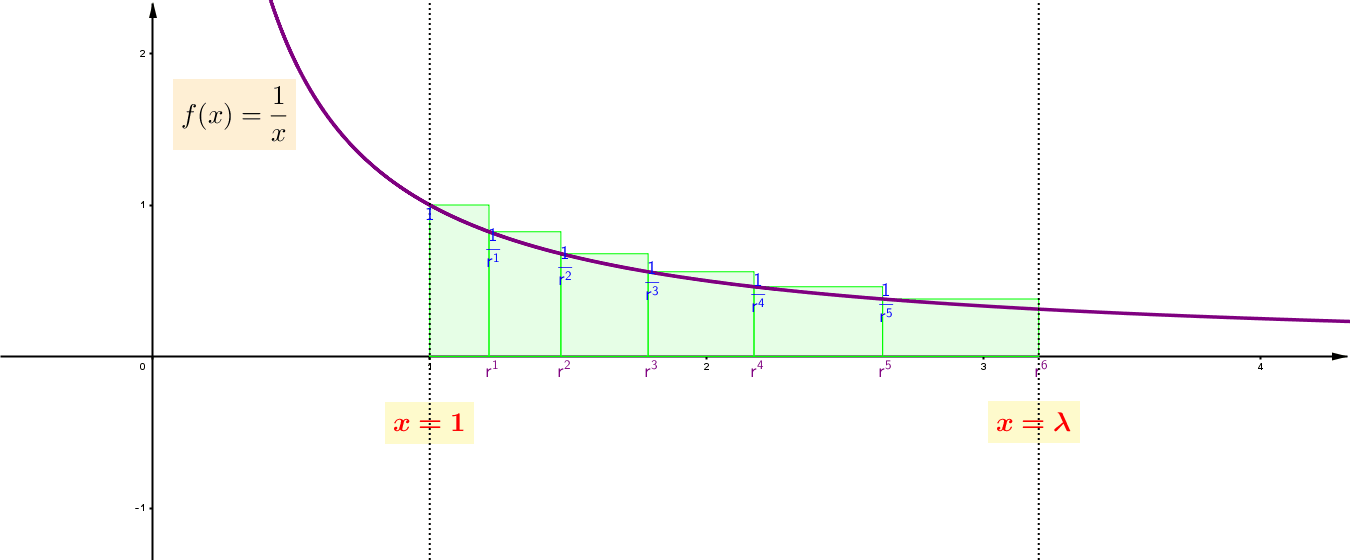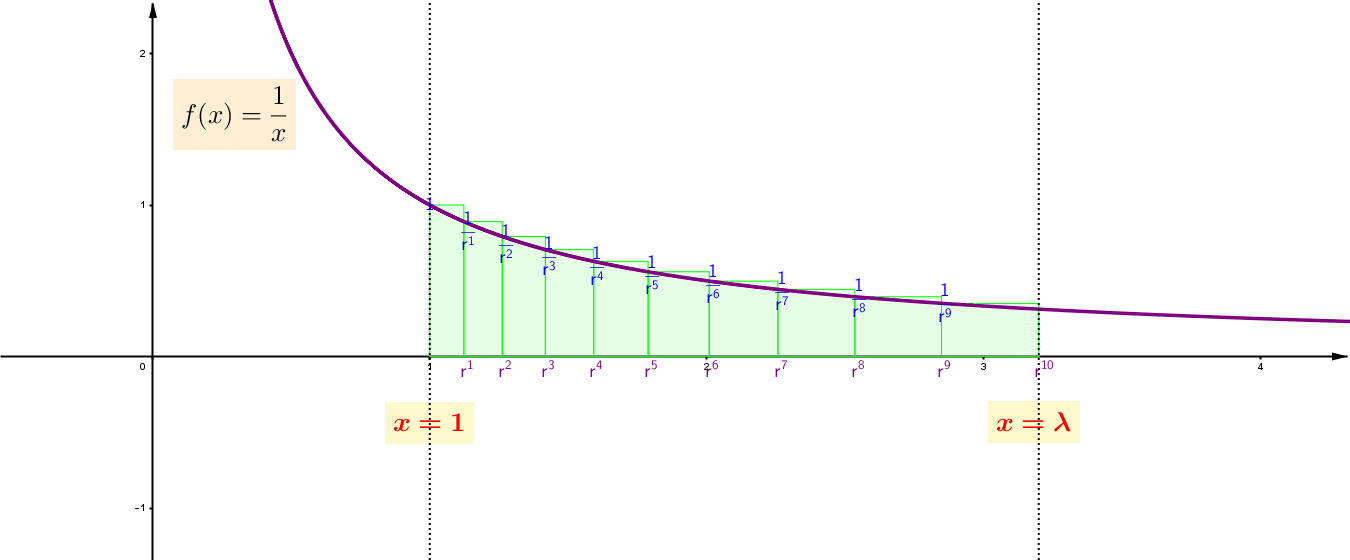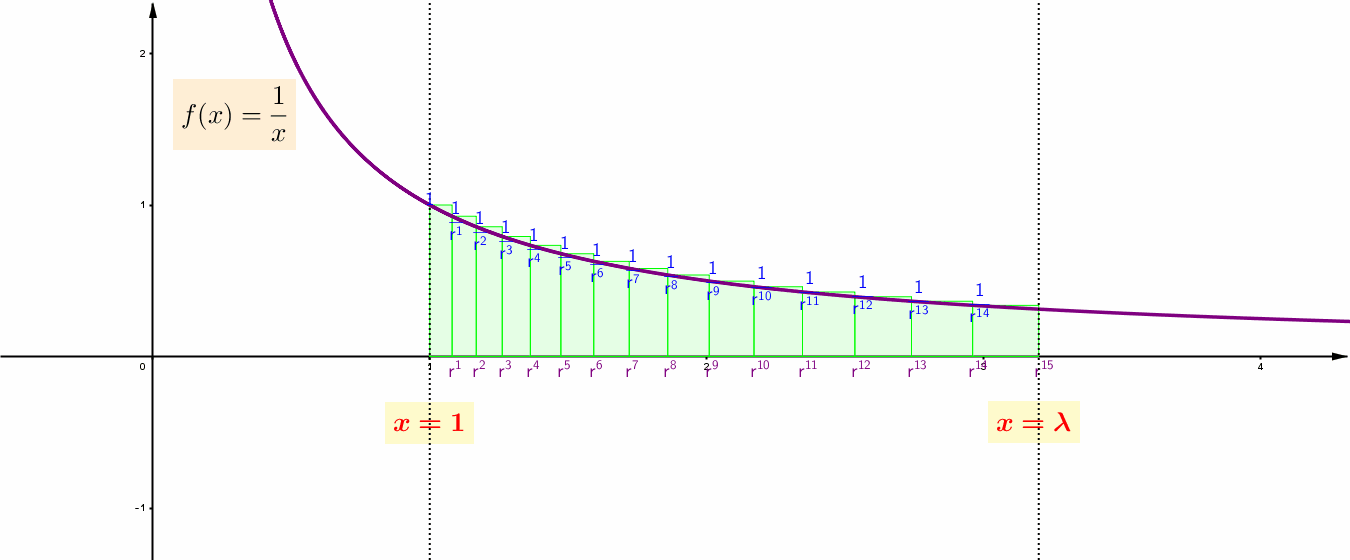
Στη συγκεκριμένη μέθοδο, το χωρίο της $y=\dfrac{\alpha}{x}$ , που περικλείεται από το γράφημά της, τον οριζόντιο άξονα, και από δύο κατάλληλες κατακόρυφες ευθείες, τις $x=1$ και $x=\lambda$ , προσεγγίζεται, κατάλληλα, από ένα άθροισμα ορθογωνίων. 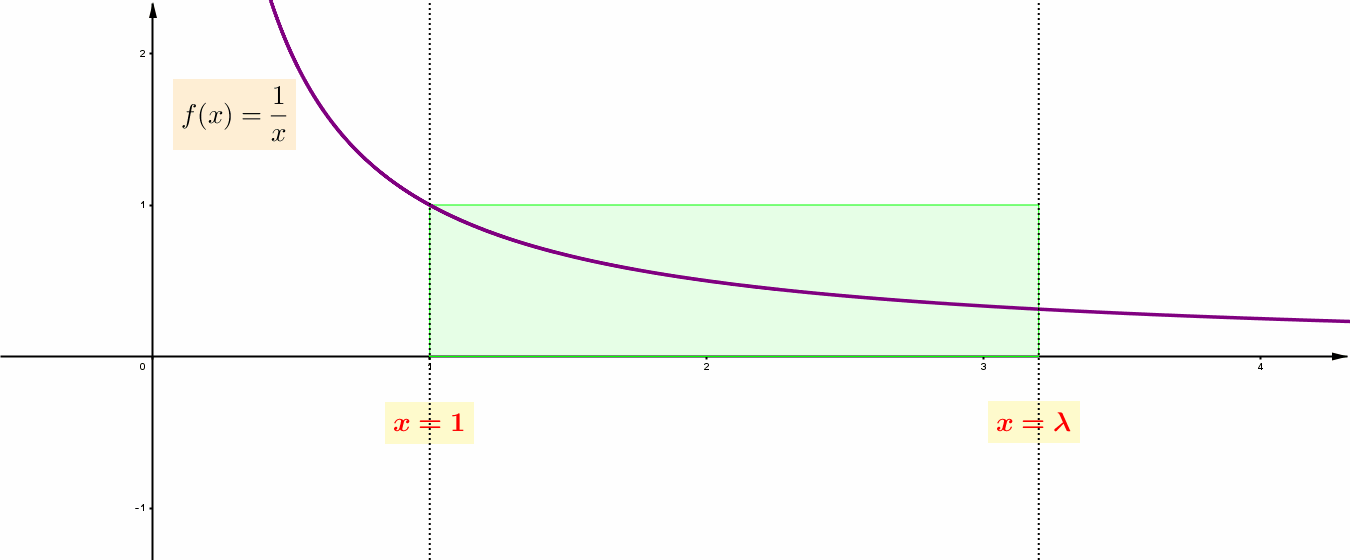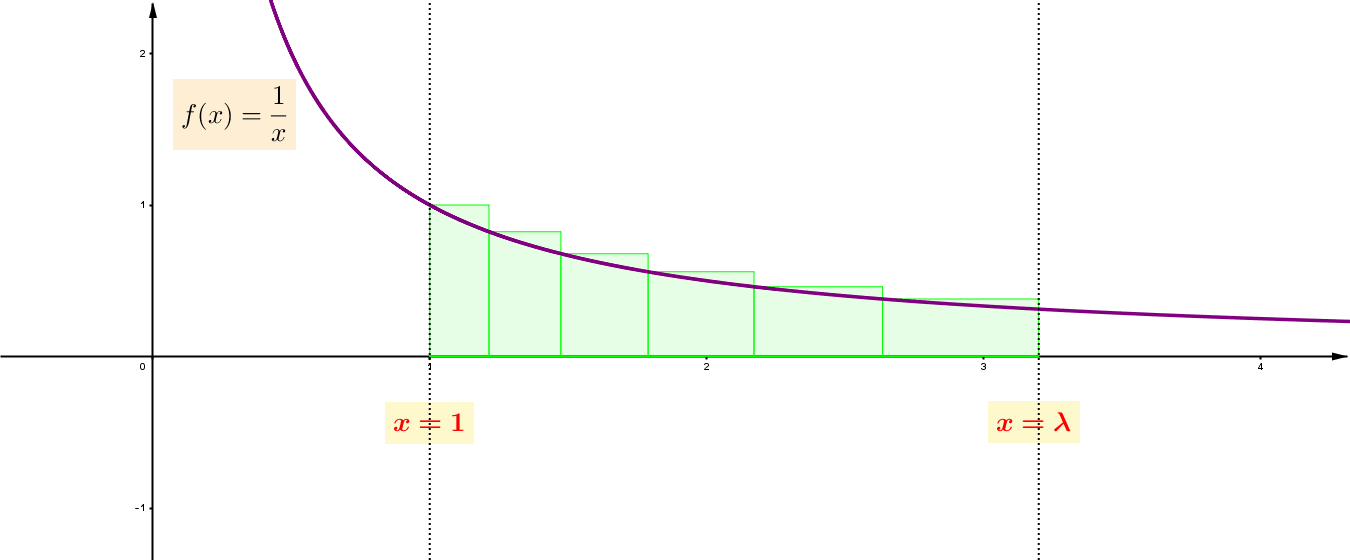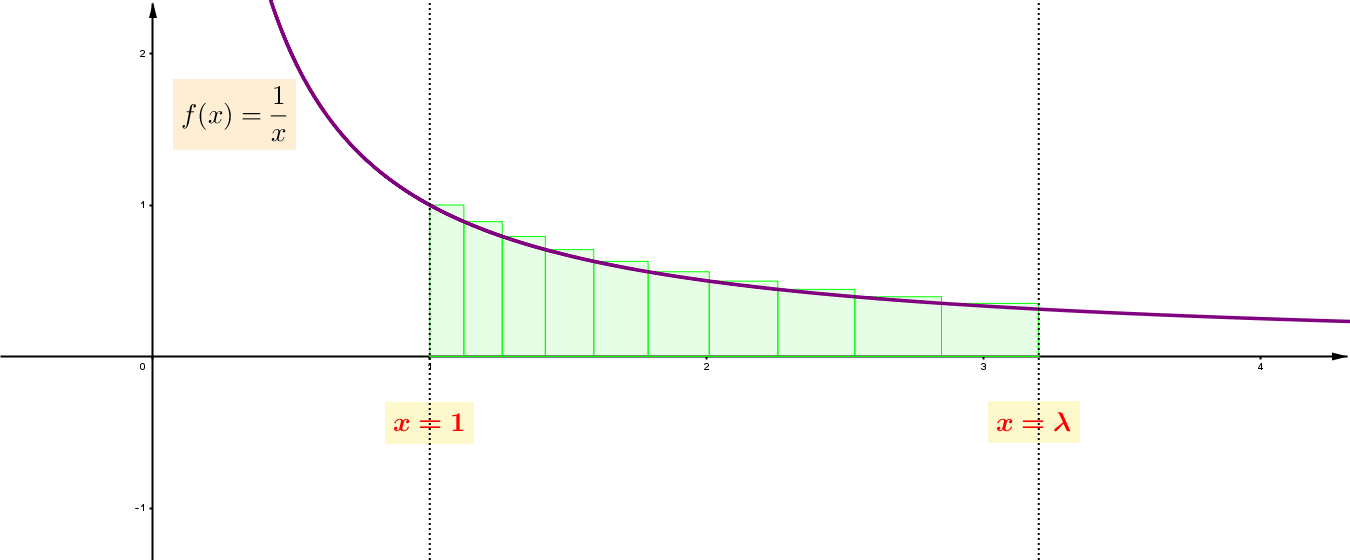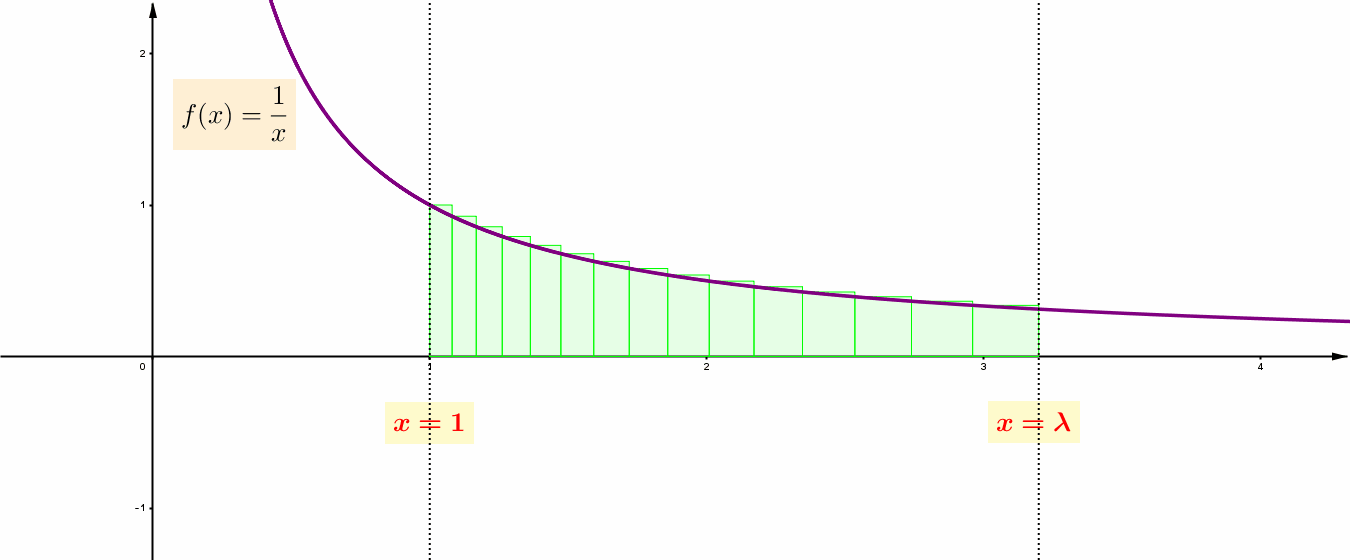(Αφού κάθε ορθογώνιο τετραγωνίζεται και επειδή, χάρη στο Πυθαγόρειο Θεώρημα, το άθροισμα δύο τετραγώνων, επίσης, τετραγωνίζεται, το παραπάνω άθροισμα των ορθογωνίων τετραγωνίζεται.)

Να παρατηρήσετε ότι το ύψος του κάθε ορθογωνίου είναι η τιμή της συνάρτησης $y=\dfrac{1}{x}$ στον αριθμό που βρίσκεται στο αριστερό άκρο της βάσης του. Το κλειδί στη μέθοδο βρίσκεται στην ακόλουθη παρατήρηση.

Σε κάθε στάδιο, οι αριθμοί του $x'x$ , στα άκρα των βάσεων των ορθογωνίων, αποτελούν γεωμετρική πρόοδο, καθώς τα μερικά αθροίσματα των εμβαδών των ορθογωνίων αποτελούν αριθμητική πρόοδο. Αυτό επιτυγχάνεται επιλέγοντας ως ακολουθία των άκρων των βάσεών τους την $1,r,r^2,\dots,r^{n-1},r^n$ , όπου $n$ φανερώνει το πλήθος των ορθογωνίων και το $r$ ικανοποιεί τη συνθήκη $r^n=\lambda$ .

Επομένως, από την κατασκευή τους, τα ύψη τους έχουν τιμές $1,\dfrac{1}{r},\dfrac{1}{r^2},\dots,\dfrac{1}{r^{n-1}}$ . Έτσι, τα αντίστοιχα ορθογώνια είναι ισεμβαδικά με εμβαδό, $E=r-1$ . Αυτό σημαίνει ότι η ακολουθία $E,2E,\dots,(n-1)E,nE$ , των μερικών αθροισμάτων των εμβαδών τους, που αναφέρθηκε προηγουμένως, αποτελεί αριθμητική πρόοδο. Μια τέτοια αντιστοιχία γεωμετρικής – αριθμητικής προόδου παραπέμπει στη λογαριθμική συνάρτηση.

Η μέθοδος αυτή, ίσως, να πρέπει να αποδοθεί στον Βέλγο Ιησουίτη Grégoire de Saint – Vincent (1584 – 1667), γνωστό με το προσωνύμιο του “κυκλοτετραγωνιστή”. Βέβαια, είναι σίγουρο ότι ο Grégoire de Saint – Vincent στηρίχθηκε σε προγενέστερες εργασίες του Γάλλου μαθηματικού και δικηγόρου Pierre de Fermat (1601 – 1665). Συγκεκριμένα, βασίστηκε στην εργασία του τελευταίου για το αντίστοιχο πρόβλημα τετραγωνισμού των γενικευμένων παραβολών. (Πρόκειται για τις καμπύλες που περιγράφονται από τον γενικό τύπο, $y=x^n.$ )

Η διαδραστική εφαρμογή

Σκιαγραφώντας τη λογαριθμική συνάρτηση

Με τη βοήθεια της παρακάτω διαδραστικής εφαρμογής, μπορείτε να δοκιμάσετε να “τετραγωνίσετε” την υπερβολή, σκια … γραφώντας την αντίστοιχη λογαριθμική συνάρτηση.

Να επιχειρήσετε να προσδώσετε στη μέθοδό σας τα χαρακτηριστικά μιας ολοένα βελτιωτικής προσεγγιστικής διαδικασίας. Όπως μπορείτε να διαπιστώσετε, στην εφαρμογή, το επιστέγασμα μιας τέτοιας διαδικασίας, αποτελεί, τελικά, τη λογαριθμική συνάρτηση, με βάση τον αριθμό $e$ του Euler.