Εισαγωγή
Ένα από τα πιο ενδιαφέροντα και συχνά μελετώμενα θέματα, ειδικά στη Γεωμετρία του Γυμνασίου, είναι οι τρεις κατασκευές για τα ύψη ενός τριγώνου.
Τα ύψη ενός τριγώνου ορίζονται ως τα τμήματα που εκτείνονται κάθετα από μια κορυφή του τριγώνου προς την απέναντι πλευρά του ή προς την προέκτασή της. Τα συγκεκριμένα ευθύγραμμα τμήματα διαδραματίζουν έναν κρίσιμο ρόλο σε πολλές γεωμετρικές εφαρμογές. Άλλωστε, ένα αξιοσημείωτο συμπέρασμα, που θα αναλύσετε στο Λύκειο, αφορά στο ότι τα τρία ύψη ενός τριγώνου διέρχονται, πάντοτε, από το ίδιο σημείο που λέγεται ορθόκεντρο.
Ωστόσο, παρά τη σχετική απλότητα της αντίστοιχης θεωρίας, πολλοί μαθητές έρχονται αντιμέτωποι με μια σειρά από προκλήσεις κατά την κατασκευή τους.
Ιδιαίτερα, στην Α΄ τάξη Γυμνασίου, σημαντική μερίδα μαθητών συναντά αρκετές δυσκολίες στη συγκεκριμένη ενότητα. Πολύ περισσότερο, στις περιπτώσεις του ορθογώνιου και του αμβλυγώνιου τριγώνου, όταν ζητείται από τους μικρούς μαθητές να σχεδιάσουν τα ύψη τους, η δυσχέρεια αυτή γίνεται ακόμη πιο εμφανής .
Στο παρόν άρθρο, θα επισημάνουμε τις πιο κοινές αστοχίες που πρέπει να αποφύγουμε όταν επιχειρούμε να σχεδιάσουμε, με τη βοήθεια του γνώμονα, τα ύψη ενός τριγώνου. Επιπλέον, θα εξετάσουμε, λεπτομερώς, τη σωστή μέθοδο κατασκευής των υψών ενός τριγώνου όταν χρησιμοποιούμε το συγκεκριμένο εργαλείο. Μάλιστα, η προσέγγιση στα παραπάνω θέματα θα γίνει με διαδραστικό τρόπο.

Γνώμονας
 Ο γνώμονας είναι ένα εργαλείο το οποίο μάς επιτρέπει να κατασκευάσουμε ορθές γωνίες (
Ο γνώμονας είναι ένα εργαλείο το οποίο μάς επιτρέπει να κατασκευάσουμε ορθές γωνίες (![]() ). Ακόμη, με τον γνώμονα, μπορούμε να επαληθεύσουμε αν μια γωνία είναι ορθή. Έτσι, ένας γνώμονας μπορεί να έχει σχήμα ορθογώνιου τριγώνου.
). Ακόμη, με τον γνώμονα, μπορούμε να επαληθεύσουμε αν μια γωνία είναι ορθή. Έτσι, ένας γνώμονας μπορεί να έχει σχήμα ορθογώνιου τριγώνου.
Με τη βοήθεια του γνώμονα, οι μαθητές μπορούν να σχεδιάσουν, με ακρίβεια, τα ύψη του τριγώνου, διασφαλίζοντας την καθετότητα μεταξύ των υψών και των αντίστοιχων πλευρών.
Ωστόσο, όπως θα αναφέρουμε στη συνέχεια, πολλά από τα πιο χαρακτηριστικά σφάλματα, στις προσπάθειες των μαθητών, ίσως να παρατηρούνται κατά το εγχείρημα της τοποθέτησης του γνώμονα στη σωστή θέση.
Συνήθεις αδυναμίες και αστοχίες μαθητών κατά τη σχεδίαση των υψών
Εδώ, θα αναλύσουμε αρκετά σημεία που χρειάζεται να επισημάνουμε προκαταβολικά. Προφανώς, πρόκειται για ζητήματα που συνδέονται με τις συνήθεις αβλεψίες των μαθητών όπως έχουν ανακύψει από τη διδακτική πράξη.
Έτσι, θα προλειάνουμε το έδαφος για να οικοδομήσουμε, καλύτερα, το συνθετικό μέρος των κατασκευών των υψών του τριγώνου.
Ελλιπής κατανόηση της έννοιας του ύψους
- Ορισμένοι μαθητές μπορεί να μην κατανοούν πλήρως τι είναι το ύψος. Έτσι, μπορεί να το συγχέουν με τη διχοτόμο της γωνίας ενός τριγώνου, ή με τη διάμεσο μιας πλευράς του, ή ακόμη και με τη μεσοκάθετο μιας πλευράς του. Ίσως η παρακάτω εικόνα να ξεδιαλύνει κάπως την κατάσταση.

- Κάποιοι μαθητές νομίζουν ότι ως βάση, για το αντίστοιχο ύψος, πρέπει να θεωρείται, πάντα, η κάτω πλευρά του τριγώνου. Απεναντίας, στην πραγματικότητα, το ύψος μπορεί να σχεδιαστεί προς οποιαδήποτε πλευρά του τριγώνου ως βάση. Η παρακάτω εικόνα είναι ενδεικτική.

Λανθασμένος προσανατολισμός για το ύψος
- Επειδή στην καθημερινότητά μας, είναι σύνηθες αρκετά αντικείμενα να έχουν πλευρές με οριζόντιο προσανατολισμό, οι μαθητές, συχνά, δυσκολεύονται να φέρουν το ύψος προς μια πλευρά που δεν είναι οριζόντια. Αυτό μπορεί να συμβεί ακόμη κι αν πρόκειται για την κάτω πλευρά του τριγώνου. Οπότε, σ’ αυτήν την περίπτωση, σχεδιάζουν το ύψος κατακόρυφα και όχι κάθετα προς την κάτω πλευρά του τριγώνου. Να παρατηρήσετε, προσεκτικά, την παρακάτω εικόνα.

- Γενικότερα, οι μαθητές, συχνά, δε σχεδιάζουν το ύψος κάθετα στη βάση. Η πιθανότερη αιτία είναι ότι η απόλυτη εφαρμογή του γνώμονα, στη σωστή θέση, δεν επιτυγχάνεται, πάντοτε, από τους μαθητές. Συνεπώς, η μια κάθετη πλευρά του γνώμονα πρέπει να βρεθεί στη βάση ή στην προέκταση της βάσης του τριγώνου. Προφανώς, η άλλη κάθετη πρέπει να διέρχεται από την αντίστοιχη κορυφή. Να δώσετε βάση στην παρακάτω εικόνα.

Λανθασμένη αντίληψη για τη σχετική θέση του ύψους ως προς το τρίγωνο
- Το γεγονός ότι το ύψος μπορεί να βρεθεί εκτός του τριγώνου, στην περίπτωση του αμβλυγώνιου τριγώνου, είναι ένα ζήτημα που απαιτεί ιδιαίτερη διδακτική προσέγγιση. Άλλωστε, το ύψος είναι το μόνο από τα δευτερεύοντα στοιχεία του τριγώνου (διάμεσοι, διχοτόμοι και ύψη) για το οποίο μπορεί να συμβεί κάτι τέτοιο. Άρα, είναι εύλογο που προκαλεί την έκπληξη αρκετών μαθητών οι οποίοι θα ανέμεναν το ύψος να βρισκόταν στο εσωτερικό του τριγώνου. Δηλαδή, θεωρούν, ως ένα βαθμό δικαιολογημένα, ότι το ύψος ενός οποιουδήποτε τριγώνου, ως στοιχείο του, αναγκαστικά, θα ανήκει σ’ αυτό. Επομένως, για γίνουν όλες οι δυνατές σχετικές του θέσεις – ως προς το τρίγωνο – κτήμα των μαθητών, χρειάζεται να τονιστεί αυτή η ιδιαιτερότητα. Άραγε, έχετε υποπέσει, ποτέ, στο λάθος που περιγράφεται στην παρακάτω εικόνα;

- Η περίπτωση όπου το ύψος συμπίπτει με κατάλληλη πλευρά του τριγώνου, όταν το τρίγωνο είναι ορθογώνιο, προβληματίζει αρκετά τους μαθητές μέχρι να αποσαφηνιστεί. Δηλαδή, φαίνεται παράδοξο το ύψος να ταυτίζεται με κάποιο από τα κύρια στοιχεία του τριγώνου όπως είναι οι πλευρές του και να μη βρίσκεται στο εσωτερικό του. Το παρακάτω σχήμα είναι ενδεικτικό.

Κατασκευή των τριών υψών τριγώνου με γνώμονα
Ενδεχομένως, με τη βοήθεια των παρακάτω κινούμενων γραφικών, να διαπιστώσετε τον σωστό τρόπο τοποθέτησης του γνώμονα για την κατασκευή των υψών ενός τριγώνου. Έτσι, θα προετοιμαστείτε, καλύτερα, για τις διαδραστικές εφαρμογές που ακολουθούν. Εκεί, πλέον, θα κληθείτε να αποπειραθείτε να υλοποιήσετε μόνοι σας τις κατασκευές αυτές.
Κατασκευή υψών σε οξυγώνιο τρίγωνο
Στο ακόλουθο κινούμενο γραφικό, να παρατηρήσετε τον τρόπο που τοποθετείται, διαδοχικά, ο γνώμονας για την κατασκευή των τριών υψών ενός οξυγώνιου τριγώνου.

Κατασκευή υψών σε αμβλυγώνιο τρίγωνο
Στη συνέχεια, ακολουθεί η περίπτωση του αμβλυγώνιου τριγώνου. Να παρατηρήσετε ότι ο γνώμονας θα τοποθετηθεί, στις προεκτάσεις των πλευρών του για τα ύψη από τις κορυφές των οξειών γωνιών του τριγώνου.

Κατασκευή υψών σε ορθογώνιο τρίγωνο
Άραγε, που βρίσκονται τα δύο ύψη που αντιστοιχούν στις κάθετες πλευρές ενός ορθογώνιου τριγώνου;
Στο ακόλουθο κινούμενο γραφικό, να παρατηρήσετε, προσεκτικά, την κατάλληλη τοποθέτηση του γνώμονα, ειδικά, για τα ύψη των κάθετων πλευρών του ορθογώνιου τριγώνου. Όπως θα διαπιστώσετε, αυτά τα δύο ύψη συμπίπτουν με τις αντίστοιχες κάθετες πλευρές του τριγώνου.

Διαδραστική εφαρμογή Geogebra για την κατασκευή υψών, με γνώμονα, σε τυχαίο τρίγωνο
Είστε έτοιμοι να δοκιμάσετε να σχεδιάσετε οι ίδιοι τα ύψη ενός τριγώνου;
Το διαδραστικό περιβάλλον της παρακάτω εφαρμογής καλύπτει όλα τα είδη τριγώνων ως προς τις γωνίες τους.
Άλλωστε, μπορείτε να μετακινήσετε τις κορυφές του τριγώνου αλλάζοντας το σχήμα του. Έτσι, σας δίνεται η δυνατότητα να πειραματιστείτε, με τρίγωνα της αρεσκείας σας, σχεδιάζοντας με τον γνώμονα τα αντίστοιχα ύψη του.
Θα αποφύγετε τα συνηθισμένα λαθάκια που, συνήθως, παρατηρούνται κατά τη σχεδίαση των υψών του τριγώνου;
Η εφαρμογή παρέχει τη δυνατότητα να ελέγξετε τις κατασκευές σας. Επιπλέον, μπορείτε, όποτε το κρίνετε απαραίτητο, να ζητήσετε βοήθεια.
Καλή ενασχόληση!
Διαδραστική εφαρμογή Geogebra για την επίλυση ενός προβλήματος σχετικό με τα ύψη τριγώνου
Στην παρακάτω εφαρμογή, γίνεται προσπάθεια οι μαθητές να συμμετάσχουν ενεργά στην επίλυση ενός προβλήματος. Ο στόχος είναι να βοηθήσουν έναν αρχιτέκτονα στην ολοκλήρωση ενός έργου. Το έργο σχετίζεται με τα όσα αναλύθηκαν παραπάνω. Συγκεκριμένα, ο αρχιτέκτονας προσπαθεί να σχεδιάσει τα κάθετα υποστυλώματα, από τις κορυφές διάφορων τριγωνικών στεγών, προς τις απέναντι πλευρές τους. Ουσιαστικά, πρόκειται για την κατασκευή των υψών ενός τριγώνου για διάφορα είδη τριγώνων. Αυτά, στην εφαρμογή, διακρίνονται μέσα από τα αντίστοιχα στάδια. Η εμπλοκή των μαθητών με τα διαδραστικά χαρακτηριστικά, που ενσωματώνει η εφαρμογή, ίσως, να ενθαρρύνει την ενασχόληση με το θέμα. Επιπλέον, παρέχονται κατάλληλα κίνητρα αλλά και αρκετές βοήθειες. Επομένως, η ολοκλήρωση των ερωτημάτων, που διαπραγματεύεται αυτό το διαδραστικό παιχνίδι, μπορεί να υλοποιηθεί σε ένα ευχάριστο, υποστηρικτικό περιβάλλον.
Εσείς αισθάνεστε έτοιμοι να βοηθήσετε τον αρχιτέκτονα ή όχι;
Μήπως ανήκετε στην κατηγορία των ανθρώπων που υποφέρουν από “υψο” … φοβία;
Αν ναι, ποιος είναι ο καλύτερος τρόπος να την υπερνικήσετε;
Καλή τύχη!
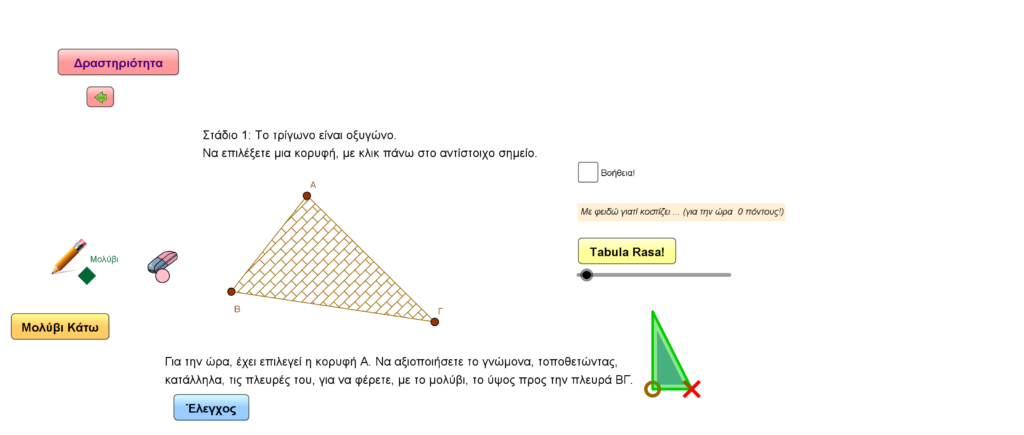
Διαδραστική εφαρμογή Geogebra για την κατασκευή των υψών τριγώνου σ’ ένα πρόβλημα.