Εισαγωγή
Το ορθόκεντρο ενός τριγώνου ορίζεται ως το σημείο τομής των φορέων (προεκτάσεων) των τριών υψών του. Πραγματικά, μπορεί να αποδειχτεί, ποικιλοτρόπως, ότι οι φορείς των τριών υψών του τριγώνου συντρέχουν, δηλαδή διέρχονται από το ίδιο σημείο.
Οι κατασκευές των τριών υψών του τριγώνου, με τη βοήθεια του γνώμονα, στις διάφορες περιπτώσεις αναφορικά με το είδος των τριγώνων, ως προς τη διάκριση με βάση τις γωνίες τους, έχουν, ήδη, διδαχθεί στο Γυμνάσιο.
Στο Λύκειο αξίζει να γίνει ιδιαίτερη αναφορά στο ορθόκεντρο.
Αλήθεια, πως θα μπορούσε να κινητοποιηθεί το ενδιαφέρον των μαθητών για τη συγκεκριμένη έννοια;
Ένα διαδραστικό παιχνίδι για το ορθόκεντρο τριγώνου
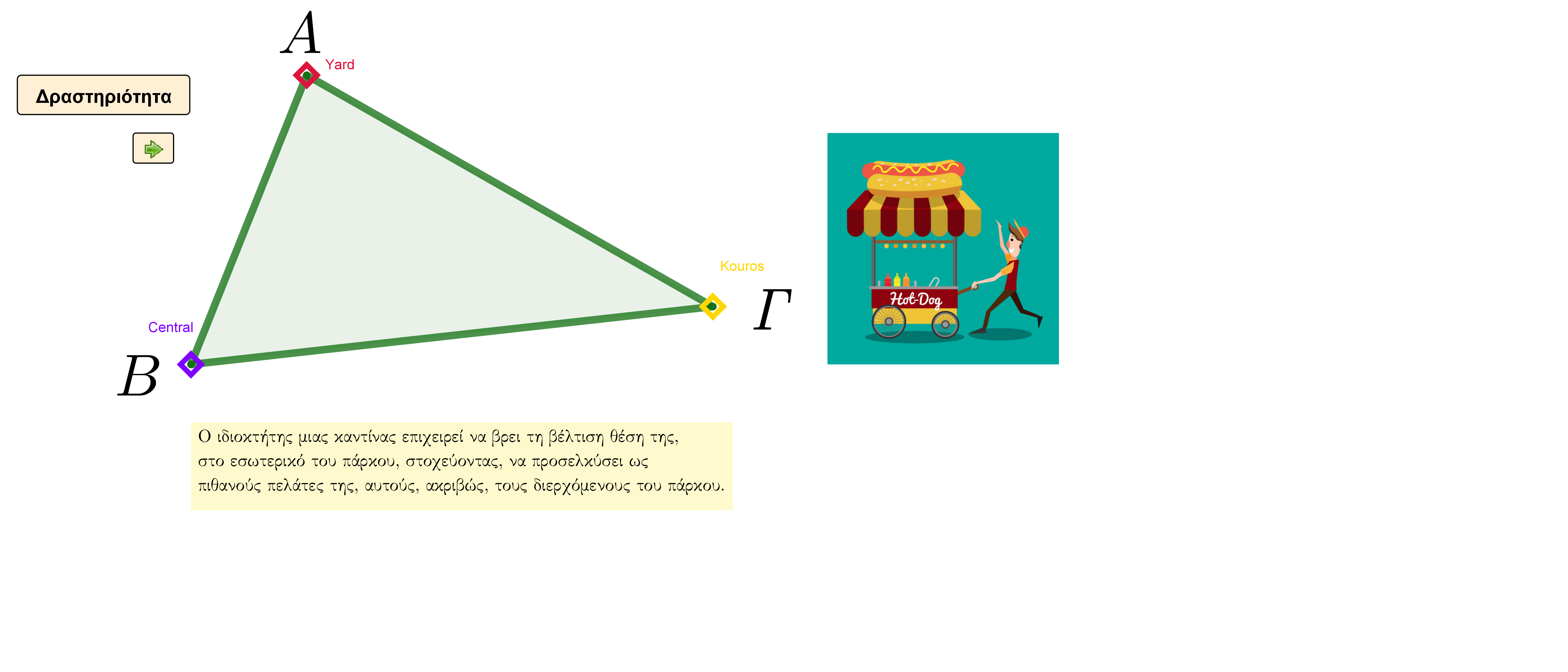
Ένα τριγωνικό πάρκο περικλείεται από τρεις πολυσύχναστους δρόμους. Στη συνένωση των δρόμων βρίσκονται τρεις καφετέριες. Κάποιοι πελάτες, αφού πιουν το ρόφημά τους, επιλέγουν να διασχίσουν το πάρκο, κατά τη συντομότερη δυνατή διαδρομή, περνώντας στον απέναντι δρόμο. Ο ιδιοκτήτης μιας καντίνας επιθυμεί να στήσει την καντίνα του στην καταλληλότερη θέση μέσα στο πάρκο έτσι, ώστε, να προσεγγίσει όσο το δυνατόν περισσότερους από τους συγκεκριμένους διερχόμενους του πάρκου. Ποια θα μπορούσε να είναι αυτή η θέση; Μπορείτε να βοηθήσετε, με τις γεωμετρικές σας γνώσεις, τον συμπαθή “γιατρό της πείνας”;
Καλή ενασχόληση!
Η απόδειξη
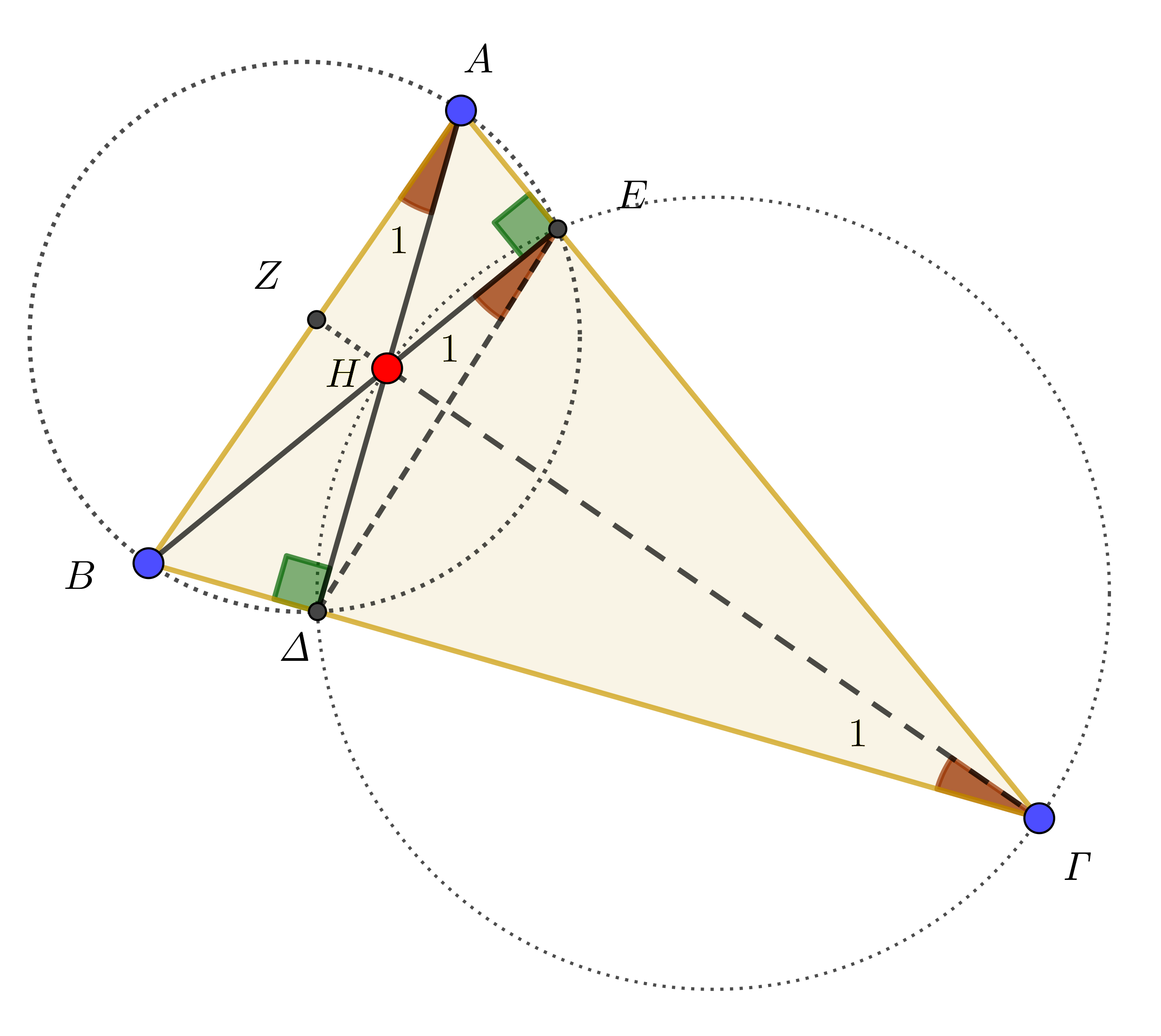
Στη Γεωμετρία, αποτελεί συνήθη τακτική, στις περιπτώσεις εκείνες όπου σκοπός είναι να αποδειχτεί ότι π.χ. τρεις ευθείες συντρέχουν, να θεωρείται το σημείο τομής των δύο ευθειών και, στη συνέχεια, να τεκμηριώνεται ότι και η τρίτη διέρχεται από το συγκεκριμένο σημείο.
Θεωρούμε, λοιπόν, τα ύψη ![]() και
και ![]() του τριγώνου
του τριγώνου ![]() . Έστω
. Έστω ![]() το σημείο τομής τους. Φέρουμε την ευθεία
το σημείο τομής τους. Φέρουμε την ευθεία ![]() , η οποία τέμνει την
, η οποία τέμνει την ![]() στο σημείο
στο σημείο ![]() . Σκοπός είναι να αποδειχτεί ότι το
. Σκοπός είναι να αποδειχτεί ότι το ![]() είναι το τρίτο ύψος, δηλαδή ότι
είναι το τρίτο ύψος, δηλαδή ότι ![]() . Παρατηρούμε ότι το τμήμα
. Παρατηρούμε ότι το τμήμα ![]() φαίνεται υπό ίσες (ως ορθές) γωνίες από τα σημεία
φαίνεται υπό ίσες (ως ορθές) γωνίες από τα σημεία ![]() και
και ![]() , γεγονός που σημαίνει ότι το τετράπλευρο
, γεγονός που σημαίνει ότι το τετράπλευρο ![]() είναι εγγεγραμμένο σε κύκλο. Έτσι,
είναι εγγεγραμμένο σε κύκλο. Έτσι, ![]() . Παρόμοια, το τετράπλευρο
. Παρόμοια, το τετράπλευρο ![]() είναι εγγεγραμμένο σε κύκλο, αφού οι απέναντι γωνίες του
είναι εγγεγραμμένο σε κύκλο, αφού οι απέναντι γωνίες του ![]() και
και ![]() είναι παραπληρωματικές (ως ορθές). Συνεπώς,
είναι παραπληρωματικές (ως ορθές). Συνεπώς, ![]() . Άρα,
. Άρα, ![]() . Εφόσον τα τρίγωνα
. Εφόσον τα τρίγωνα ![]() και
και ![]() έχουν δύο γωνίες ίσες μία προς μία (
έχουν δύο γωνίες ίσες μία προς μία (![]() και
και ![]() ), προκύπτει ότι θα έχουν και τις τρίτες γωνίες τους ίσες μία προς μία, δηλαδή ότι
), προκύπτει ότι θα έχουν και τις τρίτες γωνίες τους ίσες μία προς μία, δηλαδή ότι ![]() .
.
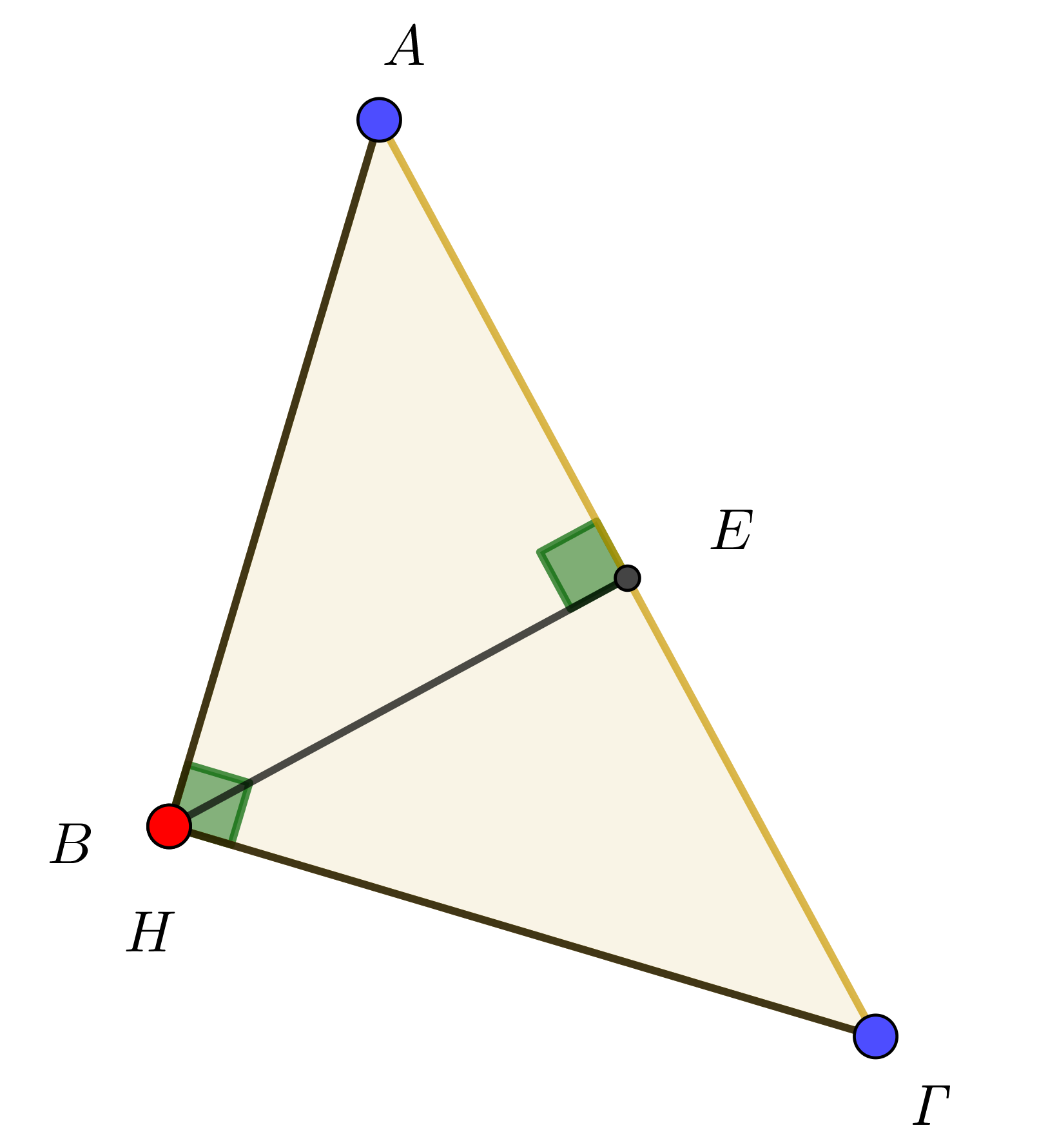
Η απόδειξη προσαρμόζεται ανάλογα στην περίπτωση αμβλυγώνιου τριγώνου,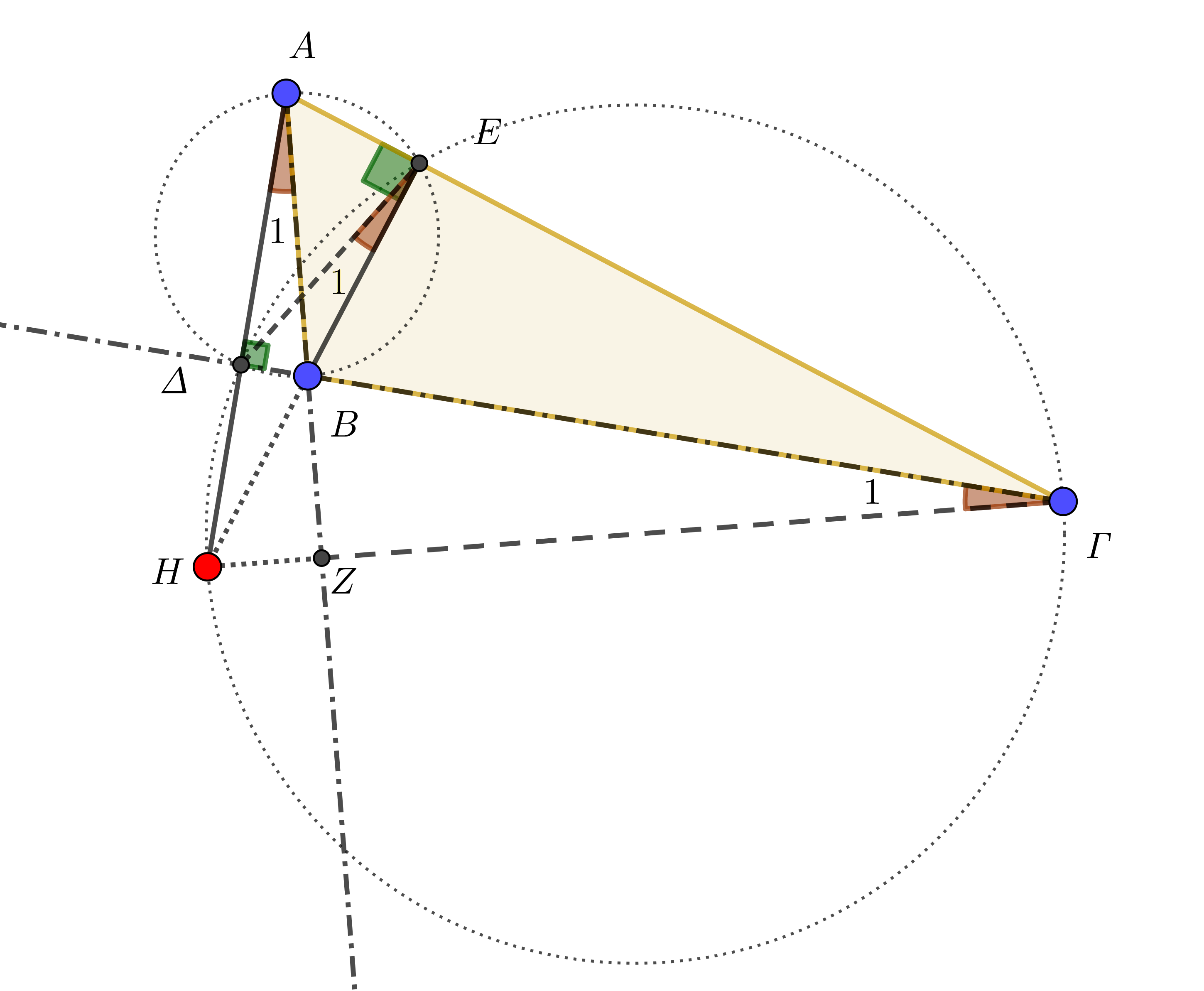
ενώ καθίσταται προφανής στην περίπτωση του ορθογώνιου τριγώνου.