Ο κύκλος και η εφαπτομένη του

Μοιραστείτε το!

Εισαγωγή

Για τα Μαθηματικά Προσανατολισμού της Β΄Λυκείου, ο κύκλος και η εφαπτομένη του, μονοπωλούν – όχι άδικα – σημαντικό μέρος του διδακτικού χρόνου. Στη συγκεκριμένη ενότητα, τα δύο πρωταρχικά γεωμετρικά σχήματα, ο κύκλος και η ευθεία, συναντώνται “οριακά”. Μάλιστα, “κοντά” στο σημείο επαφής τους, δύσκολα κανείς θα μπορούσε να τα “διαχωρίσει”. Ας μην υποτιμάται η σημασία της τελευταίας παρατήρησης.

Το γεγονός ότι σ’ ένα σημείο ενός καμπυλόγραμμου σχήματος μπορεί να “προσδεθεί” ένα ευθύγραμμο σχήμα δεν είναι διόλου ευκαταφρόνητο. Μ’ αυτόν τον τρόπο, έχει επιτευχθεί η προσέγγισή του, έστω “κοντά” στην “περιοχή” του σημείου, από ένα απλούστερο σχήμα, που, ενδεχομένως, να μπορούσε να μελετηθεί ευκολότερα.

Βέβαια, εκτός των άλλων, η ενότητα αποτελεί και μια πρώτης τάξης ευκαιρία για επανάληψη. Εδώ, αναδεικνύονται οι συνδέσεις των διάφορων εννοιών. Ειδικά, από το κεφάλαιο της ευθείας, αξιοποιούνται, λιγότερο ή περισσότερο, τα σπουδαιότερα αποτελέσματα.

Κύκλος με κέντρο την αρχή των αξόνων – Εφαπτομένη

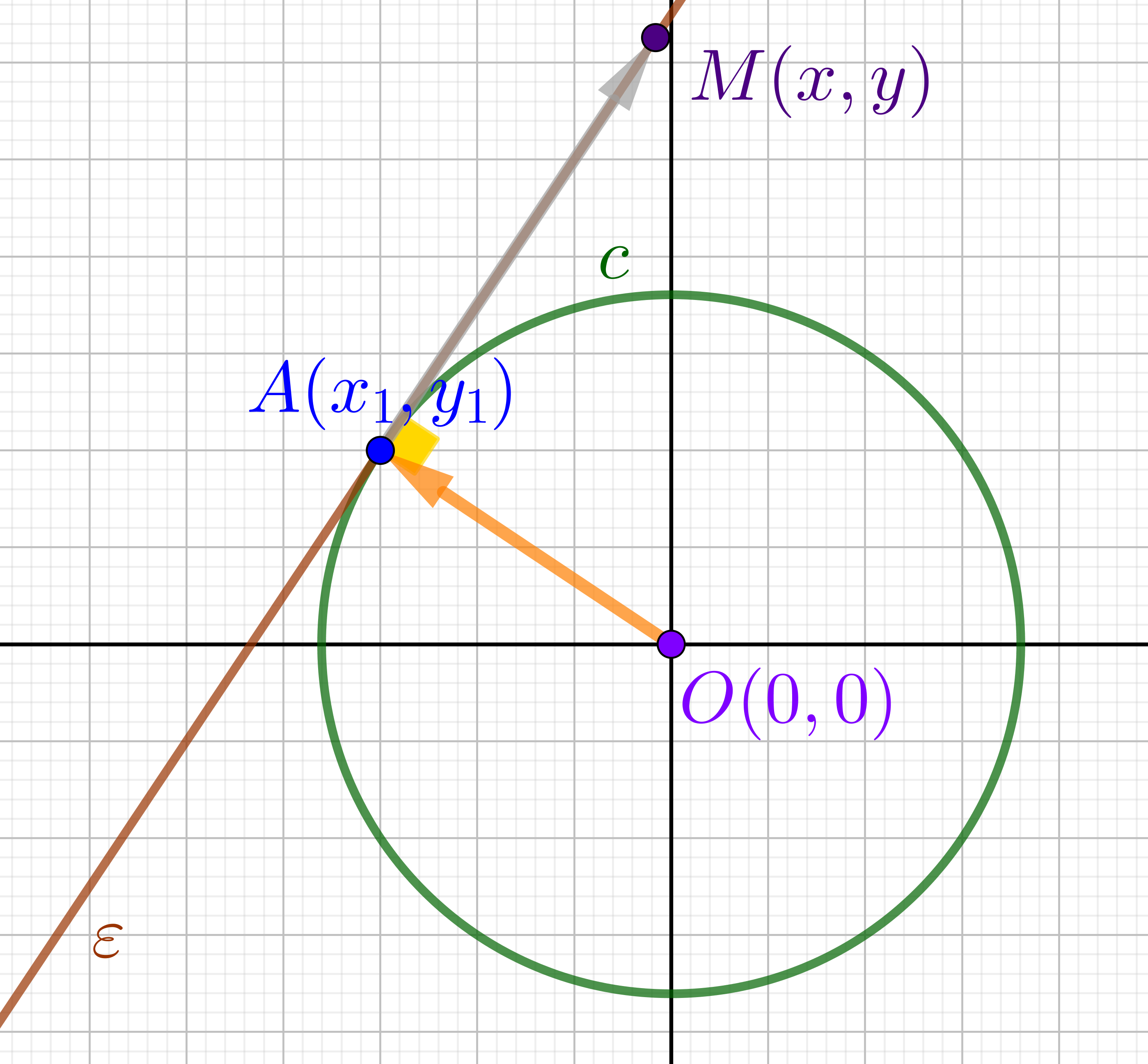
Αρχικά, στην απλούστερη περίπτωση ενός κύκλου, $c$ , κέντρου $O(0,0)$ , με εξίσωση $x^2+y^2=\rho^2$ , μπορεί να αποδειχτεί ότι η εφαπτομένη του, στο σημείο του $A(x_1,y_1)$ , δίνεται από τον τύπο $xx_1+yy_1=\rho^2$ .

Η ακόλουθη απόδειξη βασίζεται σε μια βασική πρόταση από τη Γεωμετρία της Α΄ Λυκείου. Σύμφωνα με τη συγκεκριμένη πρόταση, η ακτίνα ενός κύκλου, που καταλήγει στο σημείο επαφής μιας εφαπτομένης του με τον κύκλο, είναι κάθετη στην εφαπτομένη.

Έστω, λοιπόν, ένα σημείο $M(x,y)$ του επιπέδου.

Το $M$ ανήκει στην εφαπτομένη $\varepsilon$ αν και μόνο αν $\overrightarrow{AM}\cdot\overrightarrow{OA}=0.$ Είναι $\overrightarrow{AM}=(x-x_1,y-y_1)$ και $\overrightarrow{OA}=(x_1,y_1)$ . Έτσι,

$\overrightarrow{AM}\cdot\overrightarrow{KA}=0.$

$(x-x_1)x_1+(y-y_1)y_1=0.$

$xx_1-x_1^2+yy_1-y_1^2=0.$

$xx_1+yy_1=x_1^2+y_1^2.$

Βέβαια, $x_1^2+y_1^2=\rho^2$ , διότι το $A(x_1,y_1)$ ανήκει στον κύκλο, γεγονός που αποδεικνύει το ζητούμενο.

Παρεμπιπτόντως, χάρη στη διαπίστωση ότι η εφαπτομένη ενός κύκλου είναι κάθετη στην ακτίνα του, η οποία καταλήγει στο σημείο επαφής, είναι δυνατόν να επικυρωθεί ένα γενικότερο συμπέρασμα. Πρόκειται για το θεώρημα που αφορά στην εξίσωση της εφαπτομένης του κύκλου, στην ευρύτερη περίπτωση όπου ο κύκλος έχει κέντρο το σημείο $K(x_0,y_0)$ . Παρόλο που ο αντίστοιχος τύπος δεν αναφέρεται στο σχολικό βιβλίο, αξίζει τον κόπο ένας σχολιασμός.

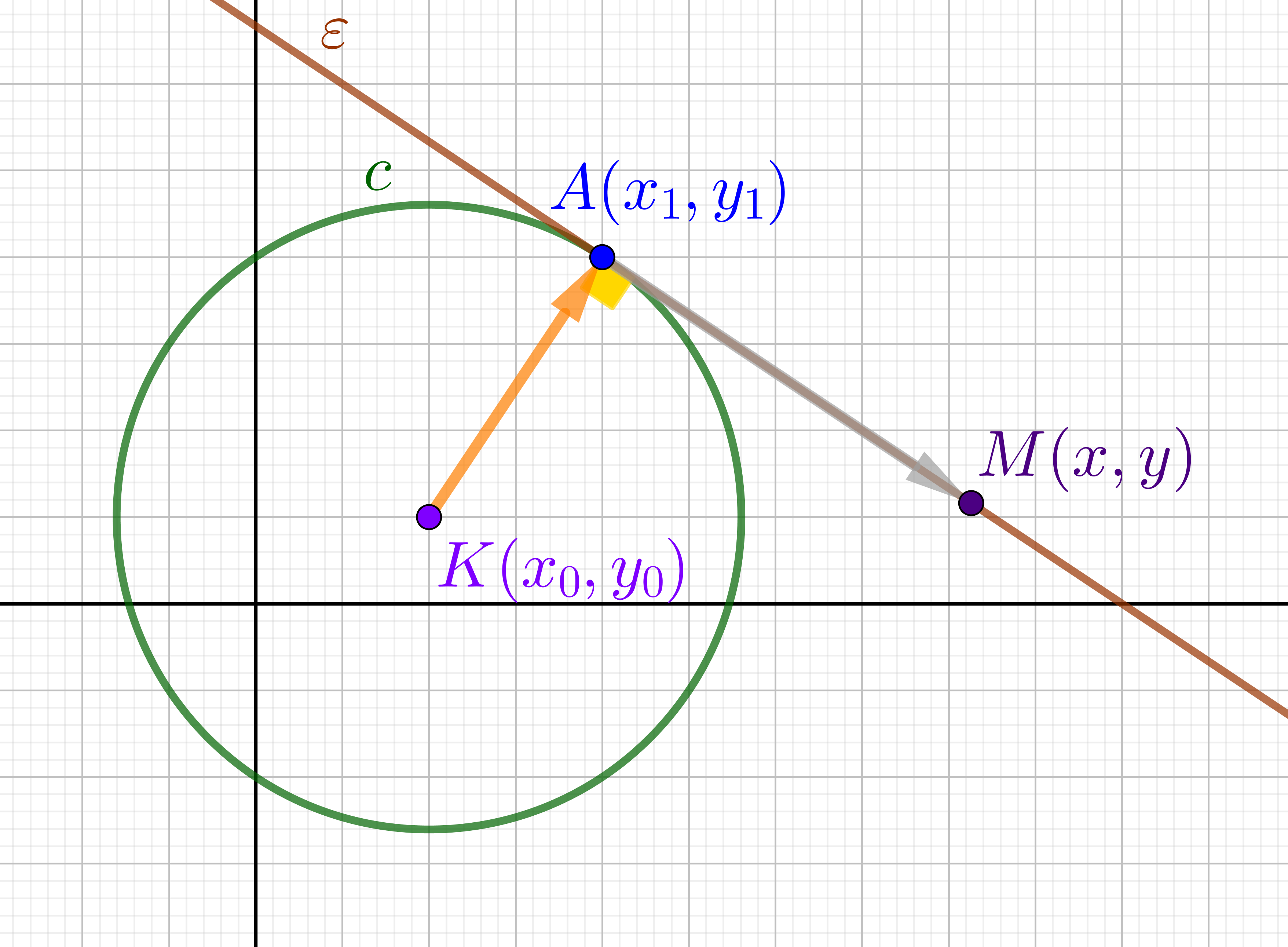
Κύκλος με κέντρο κάποιο σημείο του επιπέδου – Εφαπτομένη

Έστω, λοιπόν, ότι ο κύκλος, $c$ , έχει εξίσωση $(x-x_0)^2+(y-y_0)^2=\rho^2$ . Τότε, θα αποδειχθεί ότι η εξίσωση της εφαπτομένης του, στο σημείο του $A(x_1,y_1)$ , δίνεται από τον τύπο, $(x-x_0)(x_1-x_0)+(y-y_0)(y_1-y_0)=\rho^2$ . Είναι προφανές ότι, με δεδομένο το προηγούμενο, το περιεχόμενο της παραπάνω παραγράφου μπορεί να ενσωματωθεί ως ειδική περίπτωση.

Επιχειρώντας την απόδειξη του τύπου θεωρούμε, όπως προηγούμενα, ένα σημείο $M(x,y)$ του επιπέδου.

Όμοια, το σημείο $M$ ανήκει στην εφαπτομένη $\varepsilon$ αν και μόνο αν $\overrightarrow{AM}\cdot\overrightarrow{KA}=0.$ Έχουμε, ακόμη, ότι, $\overrightarrow{AM}=(x-x_1,y-y_1)$ και $\overrightarrow{KA}=(x_1-x_0,y_1-y_0)$ . Άρα,

$\overrightarrow{AM}\cdot\overrightarrow{KA}=0.$

$(x-x_1)(x_1-x_0)+(y-y_1)(y_1-y_0)=0.$

$(x-x_0+x_0-x_1)(x_1-x_0)+(y-y_0+y_0-y_1)(y_1-y_0)=0.$

$(x-x_0)(x_1-x_0)-(x_1-x_0)^2+(y-y_0)(y_1-y_0)-(y_1-y_0)^2=0.$

$(x-x_0)(x_1-x_0)+(y-y_0)(y_1-y_0)=(x_1-x_0)^2+(y_1-y_0)^2.$

Όμως, $(x_1-x_0)^2+(y_1-y_0)^2=\rho^2$ , διότι το $A(x_1,y_1)$ ανήκει στον κύκλο. Το τελευταίο ολοκληρώνει την απόδειξη του συμπεράσματος.

Μια εξίσωση $x^2+y^2+Ax+By+{\it\Gamma}=0$ , στην περίπτωση που παριστάνει κύκλο, μπορεί να μετασχηματιστεί, με τη μέθοδο της συμπλήρωσης τετραγώνου, στη μορφή $(x-x_0)^2+(y-y_0)^2=\rho^2$ . Επομένως, τελικά, το πρόβλημα της εξίσωσης της εφαπτομένης του κύκλου, σ’ ένα σημείο του, έχει επιλυθεί στη γενικότητά του.

Βοηθητικά συμπεράσματα

Ωστόσο, όπως προαναφέρθηκε, ο κύκλος και η εφαπτομένη του, προσφέρονται περισσότερο για να ανασύρουν οι μαθητές τις θεμελιώδεις διαδικασίες που έχουν διδαχθεί στα προηγούμενα. Μια στείρα εφαρμογή των προηγούμενων τύπων, παρόλο που προσφέρει τον άμεσο προσδιορισμό της εξίσωσης της εφαπτομένης ενός κύκλου, ενδεχομένως να αποστερεί αυτή τη δυνατότητα. Επίσης, περιορίζει σημαντικά το πεδίο των γεωμετρικών παραστάσεων των μαθητών. Αντίθετα, διδακτικά, μάλλον προκρίνεται η αξιοποίηση των προγενέστερων γνώσεων σε συνδυασμό με μια περισσότερο γεωμετρική προσέγγιση.

Ενδεικτικά, ο τύπος της απόστασης δύο σημείων, που δεν είναι τίποτε περισσότερο από το Πυθαγόρειο Θεώρημα, ο συντελεστής διεύθυνσης ευθείας που διέρχεται από δύο σημεία, ή με άλλα λόγια η εφαπτομένη της γωνίας της που σχηματίζει με τον οριζόντιο άξονα, η συνθήκη καθετότητας / παραλληλίας δύο ευθειών, η εξίσωση ευθείας που διέρχεται από γνωστό σημείο και έχει δεδομένο συντελεστή διεύθυνσης, η εύρεση σημείου ως σημείο τομής δύο ευθειών, με επίλυση του αντίστοιχου γραμμικού συστήματος που οι ευθείες ορίζουν, η μεσοκάθετος ενός τμήματος ως το σύνολο όλων των σημείων του επιπέδου που ισαπέχουν από τα άκρα του, είναι μερικά από τα “όπλα”, τα οποία εφοδιάζουν τη φαρέτρα των μαθητών για την αντιμετώπιση των προβλημάτων από τη συγκεκριμένη ενότητα.

Η διαδραστική εφαρμογή

Η ακόλουθη εφαρμογή, ίσως να μπορούσε, ως ένα βαθμό, να αποτελέσει μία διαδραστική εκδοχή ορισμένων βασικών ασκήσεων πάνω στη συγκεκριμένη ενότητα. Θα έχετε τη δυνατότητα να εξασκηθείτε με πολλά από αυτά που αναφέρθηκαν στην προηγούμενη παράγραφο.

Φυσικά, σε κάθε βήμα της εφαρμογής, μπορείτε να ελέγξετε τις απαντήσεις σας. Επιπλέον, παρέχονται χρήσιμες υποδείξεις – βοήθειες που προσφέρονται μέσα από το αλληλεπιδραστικό περιβάλλον της εφαρμογής. Ωστόσο, καθώς απώτερος στόχος είναι να πετύχετε τη μέγιστη δυνατή βαθμολογία, καλό θα ήταν να μην κάνετε κατάχρηση αυτών των υποδείξεων τουλάχιστον μετά από λίγη εξάσκηση. Να εμπλακείτε με όλα τα στάδια της εφαρμογής ακόμη και με τα περισσότερο σύνθετα.

Καλή ενασχόληση!

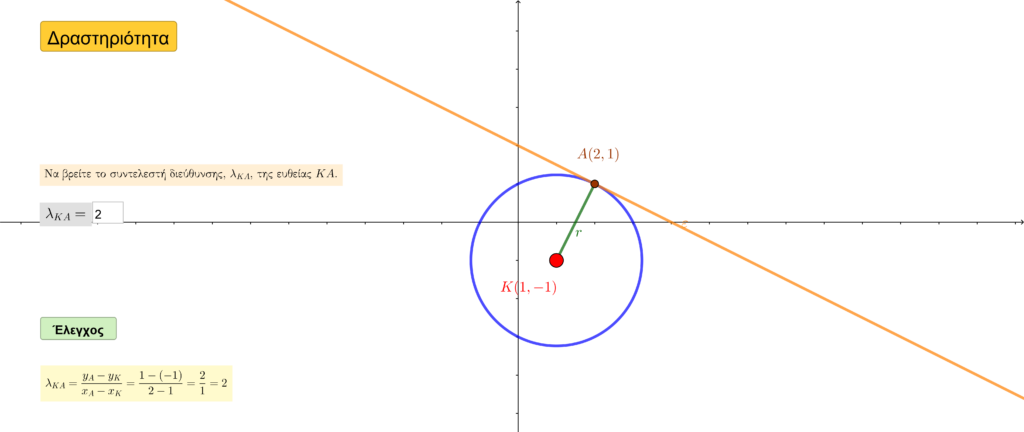
Διαδραστική εφαρμογή στον κύκλο και την εφαπτομένη του

Διαδραστικές ασκήσεις στον κύκλο και στην εφαπτομένη

Ακολουθούν τρεις διαδραστικές εφαρμογές (H5P). Η πρώτη, κατά σειρά, ελέγχει τους βασικούς τύπους της θεωρίας στην ενότητα της εφαπτομένης του κύκλου. Οι δύο τελευταίες αποτελούν προσαρμογή δύο αντίστοιχων ασκήσεων του σχολικού βιβλίου στη σχετική ενότητα.