Εισαγωγή
Στην καθημερινότητά μας, σε αρκετές περιπτώσεις, καλούμαστε να υπολογίσουμε ή έστω να εκτιμήσουμε εμβαδά διάφορων βασικών ευθύγραμμων σχημάτων.
Για παράδειγμα, στις 22 Ιουλίου 2023, στο Ολυμπιακό Στάδιο (ΟΑΚΑ), πραγματοποιήθηκε η συναυλία των Guns N’ Roses.
Άραγε, πόσοι περίπου θεατές να βρέθηκαν στον διατιθέμενο χώρο του χλοοτάπητα δηλαδή σ’ ένα ορθογώνιο με διαστάσεις, περίπου, ![]() ;
;
Είναι φανερό, ότι, για να απαντήσουμε σε τέτοια ερωτήματα, χρειάζεται, πρώτα απ’ όλα, να είμαστε σε θέση να υπολογίσουμε την έκταση του παραπάνω χωρίου. Από τη στιγμή που το παραπάνω ορθογώνιο καλύπτει μια επιφάνεια ![]() , τότε, μια εκτίμηση για το πλήθος του κόσμου εκεί θα μπορούσε να είναι γύρω στις
, τότε, μια εκτίμηση για το πλήθος του κόσμου εκεί θα μπορούσε να είναι γύρω στις ![]() , υποθέτοντας ότι, σε κάθε
, υποθέτοντας ότι, σε κάθε ![]() , βρίσκονταν, περίπου,
, βρίσκονταν, περίπου, ![]() θεατές.
θεατές.
Γενικότερα, για ένα ευθύγραμμο σχήμα, όπως ένα τρίγωνο, ένα τετράγωνο, ένα ορθογώνιο κ.ά., κάποιες φορές ενδιαφερόμαστε να βρούμε πόση έκταση καταλαμβάνει.
Για να αντιμετωπιστούν τέτοια προβλήματα, είναι απαραίτητη η κατανόηση του εμβαδού.
Ενδεικτικά,
- Όταν θέλουμε να στρώσουμε, στο πάτωμα ενός δωματίου, ένα καινούριο χαλί ή όταν θέλουμε να αγοράσουμε, για κάποιο τοίχο, ταπετσαρία, πρέπει πρώτα να υπολογίσουμε πόσα τετραγωνικά μέτρα χρειαζόμαστε.
- Σε ένα έργο, στο σχέδιο ή στη ζωγραφική, η σωστή εκμετάλλευση του διαθέσιμου χώρου, απαιτεί ορθή αντίληψη της έκτασης των επιφανειών. Τέτοιοι υπολογισμοί βοηθούν στη συμμετρία και στην καλαισθησία των στοιχείων του έργου.
- Σε αθλητικούς χώρους, όπως γήπεδα ποδοσφαίρου ή μπάσκετ, τα μήκη διάφορων γραμμών, στα όρια αυτών των γηπέδων, στηρίζονται σε υπολογισμούς εμβαδών.
- Σε παιχνίδια στρατηγικής, ψηφιακά ή επιτραπέζια, πολλές φορές καλούμαστε να «καλύψουμε» συγκεκριμένες επιφάνειες ή να τοποθετήσουμε πλακίδια με βάση το εμβαδό.
Σε προηγούμενες τάξεις, γνωρίσατε το μέγεθος του εμβαδού – όπως και το μέγεθος της περιμέτρου – στο πλαίσιο πραγματικών καταστάσεων και προβλημάτων. Έτσι, ακολουθώντας μια πιο διαισθητική και πρακτική διαδρομή, οδηγηθήκατε σε τρόπους υπολογισμού εμβαδών.
Στη συνέχεια του άρθρου, αφού γίνει μια σύντομη ιστορική αναφορά, θα γνωρίσετε τα αξιώματα του εμβαδού και θα δείτε πώς αυτά αξιοποιούνται κατά την αναζήτηση και την απόδειξη των τύπων υπολογισμού των εμβαδών στα βασικά ευθύγραμμα σχήματα. Τέλος, σάς περιμένουν διαδραστικές ασκήσεις, για να εφαρμόσετε όσα μάθατε.
Μια σύντομη ιστορική αναφορά
Για τα Αρχαία Ελληνικά Μαθηματικά, η έννοια του εμβαδού, εκτός από τις πρακτικές εφαρμογές, ίσως, να αποτέλεσε μία αναγκαστική επιλογή αξιωματικής θεμελίωσης. Η ανακάλυψη των άρρητων αριθμών και το καίριο πλήγμα που κατάφεραν στα Μαθηματικά της εποχής ανέτρεψαν την παντοδυναμία της Αριθμοθεωρίας. Έτσι, με την «αποκαθήλωση» του αριθμού, στη δύση της εποχής των Πυθαγορείων, η θεωρία των εμβαδών, ενδεχομένως, να προβάλλει ως ένας εναλλακτικό μέσο οικοδόμησης του μαθηματικού υπόβαθρου.
Έτσι, πριν ακόμα καθιερωθεί η έννοια των άρρητων αριθμών, οι αρχαίοι Έλληνες μαθηματικοί, όπως ο Ευκλείδης, προσπάθησαν να περιχαρακώσουν τη Γεωμετρία. Ενδεχομένως, στη φαρέτρα τους, τα σχήματα και οι μετασχηματισμοί τους να αποτελούσαν ένα προστατευτικό κέλυφος ικανό να προφυλάξει τα τρωτά αριθμητικά πλαίσια. Άλλωστε, η έννοια του εμβαδού – και η δυνατότητα να μετατρέπεται ένα σχήμα σε άλλο με ίδιο εμβαδόν – αποτέλεσε, για τους μαθηματικούς της εποχής, την πρώτη ύλη για να τεκμηριώσουν ακόμα και πασίγνωστα θεωρήματα!
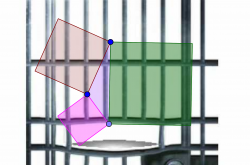
Αναγνωρίζετε τις γεωμετρικές αναφορές στο περίφημο Πυθαγόρειο Θεώρημα;
Στοιχεῖα Εὐκλείδου, Πρότασις μζ΄ (47)
Ἐν τοῖς ὀρθογωνίοις τριγώνοις τὸ ἀπὸ τῆς τὴν ὀρθὴν γωνίαν ὑποτεινούσης πλευρᾶς τετράγωνον ἴσον ἐστὶ τοῖς ἀπὸ τῶν τὴν ὀρθὴν γωνίαν περιεχουσῶν πλευρῶν τετραγώνοις.

Αξιώματα Εμβαδού
Για να γίνει η μετάβαση, από τη διαισθητική προσέγγιση της εισαγωγής, στους γεωμετρικούς ορισμούς και τις ιδιότητες του εμβαδού θα χρειαστεί ένα σύνολο αξιωμάτων. Γενικά, για μία έννοια, τα αξιώματα είναι προτάσεις που επιλέγονται, αναπόδεικτα, για να εκφράσουν τις βασικές παραδοχές της. Δηλαδή, πρόκειται για ορισμένες πρωταρχικές απαιτήσεις που, συνήθως, αντανακλούν τη φυσική ερμηνεία της έννοιας. Σίγουρα, αυτές οι αναγκαίες προϋποθέσεις συμβαδίζουν με τον σκοπό που εξυπηρετεί η έννοια.
Ως αποτέλεσμα, τις περισσότερες φορές, οι προτάσεις των αξιωμάτων δείχνουν αναμενόμενες. Βέβαια, η αλληλουχία αυτών των προτάσεων πρέπει να διέπεται από ανεξαρτησία και συνέπεια.
Ας δούμε, λοιπόν, αναλυτικά τα τρία αξιώματα για την έννοια του εμβαδού.
Αξίωμα 1 : Μονάδα μέτρησης
Το τετράγωνο πλευράς ![]() έχει εμβαδό ίσο με
έχει εμβαδό ίσο με ![]() .
. Το αξίωμα αυτό προτάσσει το παραπάνω τετράγωνο ως μια υποψήφια επιλογή για τη μονάδα μέτρησης εμβαδού. Άλλωστε, κάθε διαδικασία μέτρησης του μεγέθους ενός αντικειμένου είναι μια διαδικασία σύγκρισής του με ένα κατάλληλο σταθερό υπόδειγμα.
Το αξίωμα αυτό προτάσσει το παραπάνω τετράγωνο ως μια υποψήφια επιλογή για τη μονάδα μέτρησης εμβαδού. Άλλωστε, κάθε διαδικασία μέτρησης του μεγέθους ενός αντικειμένου είναι μια διαδικασία σύγκρισής του με ένα κατάλληλο σταθερό υπόδειγμα.
Τι προσφορότερο από το μοναδιαίο τετράγωνο να διαδραματίσει τον ρόλο του προτύπου σύγκρισης εμβαδών;
Αξίωμα 2: Διαδικασία σύγκρισης
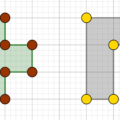
Αν μια πολυγωνική επιφάνεια διαμερίζεται σε επιμέρους πολυγωνικά χωρία ή πολυγωνικές επιφάνειες, χωρίς κοινά εσωτερικά σημεία, τότε, το εμβαδό της είναι μη αρνητικός αριθμός και ισούται με το άθροισμα των εμβαδών των επιμέρους πολυγωνικών χωρίων / πολυγωνικών επιφανειών. Οπότε, με βάση το προηγούμενο αξίωμα, στο παραπάνω πεντάγωνο, που διαμερίζεται στο τρίγωνο
Οπότε, με βάση το προηγούμενο αξίωμα, στο παραπάνω πεντάγωνο, που διαμερίζεται στο τρίγωνο ![]() και στα τετράπλευρα
και στα τετράπλευρα ![]() και
και ![]() , προκύπτει ότι το εμβαδό του ισούται με το άθροισμα των εμβαδών των
, προκύπτει ότι το εμβαδό του ισούται με το άθροισμα των εμβαδών των ![]() και
και ![]() .
.
Πλέον, χάρη σ’ αυτό το αξίωμα, μπορούν να συσχετιστούν τα εμβαδά διάφορων πολυγωνικών επιφανειών. Έτσι, το δεύτερο αξίωμα, σε συνδυασμό με το πρώτο, είναι ικανά να μετουσιώσουν την έννοια του εμβαδού σε ένα αριθμητικό μέγεθος ακολουθούμενο από τη μονάδα μέτρησης.
Παράδειγμα
Ενδεικτικά, για να γίνει κατανοητή η τελευταία παρατήρηση, να αποπειραθείτε να υπολογίσετε το εμβαδό ενός ορθογωνίου με βάση ![]() και ύψος
και ύψος ![]() .
.  Ωστόσο, να μη βιαστείτε να καταφύγετε στον γνωστό τύπο για το εμβαδό ενός ορθογωνίου ως το γινόμενο της βάσης του επί το ύψος του.
Ωστόσο, να μη βιαστείτε να καταφύγετε στον γνωστό τύπο για το εμβαδό ενός ορθογωνίου ως το γινόμενο της βάσης του επί το ύψος του.
Για την ώρα, μπορείτε να αξιοποιήσετε μόνο τα προηγούμενα αξιώματα. Μέχρι στιγμής, αυτά αποτελούν τα μόνα συμπεράσματα σχετικά με την έννοια του εμβαδού. Τα υπόλοιπα αποτελέσματα, πολλά από τα οποία έχετε διδαχθεί στο παρελθόν, θα ανακύπτουν, σταδιακά, καθώς οικοδομείται η θεωρία των εμβαδών.
Επομένως, μοιάζει με μονόδρομο το ορθογώνιο, με βάση ![]() και ύψος
και ύψος ![]() , να διαμεριστεί σε δύο τετράγωνα πλευράς
, να διαμεριστεί σε δύο τετράγωνα πλευράς ![]() . Όμως, από το Αξίωμα 1, τα τετράγωνα αυτά έχουν εμβαδό ίσο με το
. Όμως, από το Αξίωμα 1, τα τετράγωνα αυτά έχουν εμβαδό ίσο με το ![]() . Άρα, από το Αξίωμα 2, το εμβαδό αυτού του ορθογωνίου ισούται με
. Άρα, από το Αξίωμα 2, το εμβαδό αυτού του ορθογωνίου ισούται με ![]() τετραγωνικές μονάδες.
τετραγωνικές μονάδες.
Αξίωμα 3: Εμβαδό καλώς ορισμένο
Ίσα πολύγωνα είναι ισεμβαδικά (ισοδύναμα). Το τρίτο αξίωμα εξασφαλίζει ότι, στην ίδια πολυγωνική επιφάνεια, δε μπορούν να αποδοθούν, για το εμβαδό της, πάνω από μία τιμές.
Το τρίτο αξίωμα εξασφαλίζει ότι, στην ίδια πολυγωνική επιφάνεια, δε μπορούν να αποδοθούν, για το εμβαδό της, πάνω από μία τιμές.
Βασικά συμπεράσματα
Με οδηγό τα παραπάνω αξιώματα θα μπορούσαμε να τεκμηριώσουμε τα πρώτα βασικά συμπεράσματα στα εμβαδά ευθύγραμμων σχημάτων.
- Όταν ένα πολυγωνικό χωρίο,
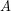 , περιέχεται σε ένα πολυγωνικό χωρίο,
, περιέχεται σε ένα πολυγωνικό χωρίο, 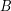 , τότε, το εμβαδό του χωρίου,
, τότε, το εμβαδό του χωρίου, 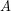 , είναι μικρότερο ή ίσο από το εμβαδό του χωρίου
, είναι μικρότερο ή ίσο από το εμβαδό του χωρίου 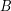 .
.
Πράγματι, το παρακάτω σχήμα είναι ενδεικτικό για το ότι το χωρίο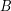 , που περιέχει, στο εσωτερικό του, το χωρίο
, που περιέχει, στο εσωτερικό του, το χωρίο 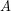 , διαμερίζεται σε δύο πολυγωνικές επιφάνειες: στο
, διαμερίζεται σε δύο πολυγωνικές επιφάνειες: στο 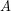 και στο συμπλήρωμα του
και στο συμπλήρωμα του 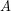 στο
στο 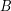 . Οπότε, το εμβαδό του
. Οπότε, το εμβαδό του 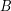 , ως το άθροισμα των εμβαδών των δύο αυτών πολυγωνικών επιφανειών (Αξίωμα 2), είναι μεγαλύτερό ή ίσο από κάθε ένα από αυτά, άρα μεγαλύτερο ή ίσο από το εμβαδό του
, ως το άθροισμα των εμβαδών των δύο αυτών πολυγωνικών επιφανειών (Αξίωμα 2), είναι μεγαλύτερό ή ίσο από κάθε ένα από αυτά, άρα μεγαλύτερο ή ίσο από το εμβαδό του 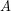 .
.

- Το εμβαδό ενός τετραγώνου πλευράς,
 , ισούται με
, ισούται με 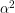 .
. Φυσικά, το συμπέρασμα απορρέει από τα Αξιώματα 1 και 2, διότι το τετράγωνο πλευράς
Φυσικά, το συμπέρασμα απορρέει από τα Αξιώματα 1 και 2, διότι το τετράγωνο πλευράς  διαμερίζεται σε
διαμερίζεται σε 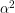 τετράγωνα τα οποία έχουν πλευρά
τετράγωνα τα οποία έχουν πλευρά 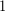 στη χρησιμοποιούμενη μονάδα μέτρησης μήκους.
στη χρησιμοποιούμενη μονάδα μέτρησης μήκους. - Το εμβαδό ενός ορθογωνίου, με διαστάσεις
 και
και 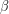 , έχει εμβαδό το γινόμενο
, έχει εμβαδό το γινόμενο  των διαστάσεων αυτών.
των διαστάσεων αυτών. Παρόμοια, το συμπέρασμα απορρέει από τα Αξιώματα 1 και 2, διότι ένα τέτοιο ορθογώνιο διαμερίζεται σε
Παρόμοια, το συμπέρασμα απορρέει από τα Αξιώματα 1 και 2, διότι ένα τέτοιο ορθογώνιο διαμερίζεται σε  τετράγωνα τα οποία έχουν πλευρά
τετράγωνα τα οποία έχουν πλευρά 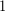 στη χρησιμοποιούμενη μονάδα μέτρησης μήκους.
στη χρησιμοποιούμενη μονάδα μέτρησης μήκους.
Κύριοι τύποι εμβαδού ευθύγραμμων σχημάτων
Άραγε, θα μπορούσαμε, με τη βοήθεια του τύπου του εμβαδού του ορθογώνιου παραλληλογράμμου, να συνάγουμε, προοδευτικά, τους τύπους για τα εμβαδά των υπόλοιπων βασικών ευθύγραμμων σχημάτων;
Ας αναζητήσουμε, λοιπόν, τους αντίστοιχους τύπους, διαδοχικά, για το πλάγιο παραλληλόγραμμο, για το τρίγωνο και για το τραπέζιο. Θα υιοθετήσουμε τον συμβολισμό, ![]() , για το εμβαδό του πολυγωνικού χωρίου,
, για το εμβαδό του πολυγωνικού χωρίου, ![]() .
.
- Πλάγιο παραλληλόγραμμο.
 Στο παραπάνω σχήμα, το παραλληλόγραμμο
Στο παραπάνω σχήμα, το παραλληλόγραμμο  , με βάση
, με βάση 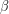 και αντίστοιχο ύψος
και αντίστοιχο ύψος  , μετασχηματίζεται στο ισεμβαδικό ορθογώνιο παραλληλόγραμμο
, μετασχηματίζεται στο ισεμβαδικό ορθογώνιο παραλληλόγραμμο  .
.
Πράγματι, το τρίγωνο που “αποκόπτεται” είναι ίσο με το τρίγωνο
που “αποκόπτεται” είναι ίσο με το τρίγωνο  που “επικολλάται”. Προφανώς, το ορθογώνιο
που “επικολλάται”. Προφανώς, το ορθογώνιο  έχει κι αυτό βάση
έχει κι αυτό βάση 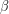 και ύψος
και ύψος  . Τελικά,
. Τελικά,
Δηλαδή, το εμβαδό ενός οποιουδήποτε παραλληλογράμμου ισούται με το γινόμενο μιας βάσης του επί το αντίστοιχο ύψος του.![Rendered by QuickLaTeX.com \[(AB{\it\Gamma\Delta})=(AB{\it\Lambda}K)=\beta\cdot\upsilon.\]](https://dkonas.sites.sch.gr/wp-content/ql-cache/quicklatex.com-d876334b32358dfbe93a68c5c54cad5a_l3.png)
-
Τρίγωνο.
Στο παραπάνω σχήμα, το τρίγωνο
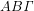 , με βάση
, με βάση 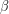 και αντίστοιχο ύψος
και αντίστοιχο ύψος  , έχει εμβαδό ίσο με το μισό του παραλληλογράμμου
, έχει εμβαδό ίσο με το μισό του παραλληλογράμμου  .
.
Πράγματι, τα τρίγωνα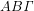 και
και  μπορεί, εύκολα, να αποδειχθεί ότι είναι ίσα. Άρα,
μπορεί, εύκολα, να αποδειχθεί ότι είναι ίσα. Άρα,  . Επίσης, το παραλληλόγραμμο
. Επίσης, το παραλληλόγραμμο  και το τρίγωνο
και το τρίγωνο 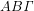 έχουν την ίδια βάση,
έχουν την ίδια βάση, 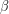 , όπως και το ίδιο ύψος,
, όπως και το ίδιο ύψος,  . Τελικά,
. Τελικά,
Δηλαδή, το εμβαδό ενός οποιουδήποτε τριγώνου ισούται με το ημιγινόμενο μιας βάσης του επί το αντίστοιχο ύψος του.![Rendered by QuickLaTeX.com \[(AB{\it\Gamma})=\frac{1}{2}\cdot\beta\cdot\upsilon.\]](https://dkonas.sites.sch.gr/wp-content/ql-cache/quicklatex.com-61cdc2768d089cff5babc2ea2266fd51_l3.png)
-
Τραπέζιο.
Στο παραπάνω σχήμα, το τραπέζιο
 , με βάσεις τις
, με βάσεις τις 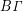 ,
, 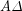 και ύψος
και ύψος  , διαμερίζεται μέσω της διαγωνίου του
, διαμερίζεται μέσω της διαγωνίου του 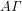 στα τρίγωνα
στα τρίγωνα 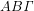 και
και  . Συνεπώς,
. Συνεπώς,
Δηλαδή, το εμβαδό ενός οποιουδήποτε τραπεζίου ισούται με το ημιγινόμενο του αθροίσματος των δύο βάσεών του επί το ύψος του.![Rendered by QuickLaTeX.com \[(AB{\it\Gamma\Delta})=(AB{\it\Gamma})+(A{\it\Gamma\Delta})=\frac{1}{2}\cdot B{\it\Gamma}\cdot\upsilon+\frac{1}{2}\cdot A{\it\Delta}\cdot\upsilon=\frac{(B{\it\Gamma}+A{\it\Delta})\cdot\upsilon}{2}.\]](https://dkonas.sites.sch.gr/wp-content/ql-cache/quicklatex.com-fc048884b006c8331013f5f322ce4ae6_l3.png)
Άλλοι τύποι για το εμβαδό τριγώνου
Σε πολλές περιπτώσεις, ενδέχεται να μην είναι βολικό να υπολογίσουμε το εμβαδό ενός τριγώνου με τον συνήθη τρόπο ως το γινόμενο μιας βάσης του επί το αντίστοιχο ύψος. Ίσως, να είναι πιο πρόσφορο, για το τρίγωνο, να καθορίσουμε την έκταση που καταλαμβάνει από διαφορετικά στοιχεία του. Παρακάτω, θα παραθέσουμε διάφορους εναλλακτικούς τύπους για το εμβαδό ενός τριγώνου.
Τριγωνομετρικός τύπος

Ο τύπος αυτός προϋποθέτει να είναι γνωστές δύο πλευρές του τριγώνου και η περιεχόμενη γωνία τους. Πράγματι, στο παραπάνω σχήμα, επιλέγοντας ως βάση την πλευρά ![]() , με αντίστοιχο ύψος το
, με αντίστοιχο ύψος το ![]() , έχουμε,
, έχουμε, ![]()
![]() , που σημαίνει ότι,
, που σημαίνει ότι, ![]()
Τύπος του Ήρωνα

Ο τύπος του Ήρωνα εκφράζει το εμβαδό ενός τριγώνου με τη βοήθεια των πλευρών του. Ειδικότερα, ![]()
![]() είναι η ημιπερίμετρος του τριγώνου
είναι η ημιπερίμετρος του τριγώνου ![]() .
.
Αν ενδιαφέρεστε για την απόδειξη του τύπου αλλά και για το γενικότερο ζήτημα της αναζήτησης ενός αντίστοιχου συμπεράσματος για το τετράπλευρο να ανατρέξετε εδώ.
Τύπος με την ακτίνα του εγγεγραμμένου του κύκλου.

Ο συγκεκριμένος τύπος εκφράζει το εμβαδό ενός τριγώνου με τη βοήθεια της ημιπεριμέτρου του καθώς και της ακτίνας του εγγεγραμμένου του κύκλου. Πρόκειται για τον τύπο, ![]()
![]() παριστάνει την ημιπερίμετρο του τριγώνου και
παριστάνει την ημιπερίμετρο του τριγώνου και ![]() την ακτίνα του εγγεγραμμένου του κύκλου.
την ακτίνα του εγγεγραμμένου του κύκλου.
Για την απόδειξη του τύπου, να παρατηρήσετε, αρχικά, ότι, στο παραπάνω σχήμα, το κέντρο, ![]() , του εγγεγραμμένου του κύκλου, απέχει από τις πλευρές του τριγώνου όσο η ακτίνα,
, του εγγεγραμμένου του κύκλου, απέχει από τις πλευρές του τριγώνου όσο η ακτίνα, ![]() , αυτού του κύκλου. Επομένως,
, αυτού του κύκλου. Επομένως, ![]()
![]()
![]() .
.
Τύπος με την ακτίνα του περιγεγραμμένου του κύκλου

Τέλος, υπάρχει τύπος που εκφράζει το εμβαδό ενός τριγώνου με τη βοήθεια των πλευρών του και της ακτίνας του περιγεγραμμένου του κύκλου.
Συγκεκριμένα, ![]()
![]() είναι η ακτίνα του περιγεγραμμένου κύκλου του τριγώνου
είναι η ακτίνα του περιγεγραμμένου κύκλου του τριγώνου ![]() . Πράγματι, στο προηγούμενο σχήμα, είναι,
. Πράγματι, στο προηγούμενο σχήμα, είναι, ![]()
![]() , διότι η εγγεγραμμένη γωνία,
, διότι η εγγεγραμμένη γωνία, ![]() , βαίνει στο ίδιο τόξο με την επίκεντρη γωνία,
, βαίνει στο ίδιο τόξο με την επίκεντρη γωνία, ![]() . Συνεπώς,
. Συνεπώς, ![]() . Οπότε,
. Οπότε, ![]()
![]()
Διαδραστικές ασκήσεις
Τι θα λέγατε να ελέγξετε τον βαθμό κατανόησης της έννοιας του εμβαδού με διαδραστικό τρόπο;
Παρακάτω, παρατίθενται ορισμένες ερωτήσεις κατανόησης και ασκήσεις εμπέδωσης κλειστού τύπου. Αυτές οι ερωτήσεις καλύπτουν ένα σημαντικό μέρος της ενότητας των εμβαδών ευθύγραμμων σχημάτων. Ακόμη, καθώς οι απαντήσεις σας υποβάλλονται, η ορθότητά τους εξετάζεται άμεσα. Επίσης, παρέχεται η σχετική ανατροφοδότηση με τα κατάλληλα σχόλια που συνοδεύουν την υποβολή της κάθε απάντησης.
Καλή ενασχόληση!