Εισαγωγή
Είναι δυνατόν να κατασκευαστούν δύο ευθύγραμμα σχήματα με ίση περίμετρο και ίσο εμβαδό στην ίδια μονάδα μέτρησης;
Το ερώτημα αυτό απασχόλησε τους μαθητές ενός τμήματος, κατά τη διάρκεια του σχολικού έτους 2020 -2021, στο μάθημα της Γεωμετρίας της Β΄ Λυκείου. Είναι αλήθεια ότι οι πρωταρχικές έννοιες της περιμέτρου και του εμβαδού των σχημάτων, πολλές φορές, μάς φέρνουν αντιμέτωπους με ενδιαφέροντα ζητήματα.
Το tetris
Για τους λάτρεις του δημοφιλούς ηλεκτρονικού παιχνιδιού tetris, τα σχήματα της παρακάτω εικόνας, λογικά, είναι αρκετά οικεία.
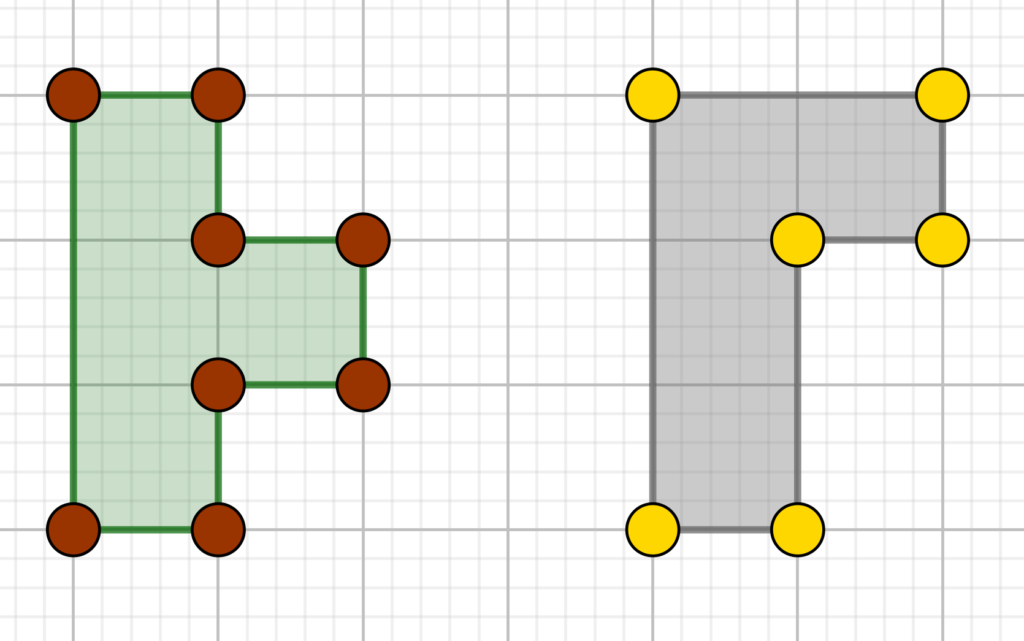
Το πρώτο είναι ένα μη κυρτό οκτάγωνο ενώ το δεύτερο είναι ένα μη κυρτό εξάγωνο. Είναι εύκολο να διαπιστώσετε ότι πρόκειται για σχήματα με ίσες περιμέτρους (![]() ) και ίσα εμβαδά (
) και ίσα εμβαδά (![]() τ.μ.).
τ.μ.).
Εύλογα, τίθεται το ερώτημα αν θα μπορούσαν να βρεθούν δύο κυρτά σχήματα με ίση περίμετρο και ίσο εμβαδό. Ακόμη, ενδιαφέρον παρουσιάζει το κατά πόσο τα ζητούμενα σχήματα θα μπορούσαν να έχουν τον ίδιο αριθμό πλευρών.
Τρίγωνο με ορθογώνιο
Διερευνώντας, λοιπόν, πιο “κλασικά” σχήματα, μπορεί να διαπιστωθεί π.χ. ότι για οποιοδήποτε τρίγωνο υπάρχει ακριβώς ένα ορθογώνιο παραλληλόγραμμο με ίση περίμετρο και ίσο εμβαδό μ’ αυτό του τριγώνου αρκεί να ικανοποιείται μια κατάλληλη ικανή και αναγκαία συνθήκη.
Πράγματι, έστω τρίγωνο περιμέτρου ![]() και εμβαδού
και εμβαδού ![]() . Για να υπάρχει ορθογώνιο παραλληλόγραμμο με ίση περίμετρο και ίσο εμβαδό με το τρίγωνο πρέπει και αρκεί να βρεθούν
. Για να υπάρχει ορθογώνιο παραλληλόγραμμο με ίση περίμετρο και ίσο εμβαδό με το τρίγωνο πρέπει και αρκεί να βρεθούν ![]() τέτοια, ώστε,
τέτοια, ώστε, ![]() και
και ![]() . Αυτό συμβαίνει αν και μόνο αν η δευτεροβάθμια εξίσωση,
. Αυτό συμβαίνει αν και μόνο αν η δευτεροβάθμια εξίσωση, ![]()
έχει λύση, δηλαδή, τελικά, αν και μόνο αν ισχύει, ![]()
Παράδειγμα
Θεωρούμε το ορθογώνιο τρίγωνο με πλευρές ![]() και
και ![]() . Τότε,
. Τότε, ![]() και
και ![]() . Επιλύοντας τη δευτεροβάθμια εξίσωση,
. Επιλύοντας τη δευτεροβάθμια εξίσωση, ![]() , προκύπτει ότι το ορθογώνιο με διαστάσεις
, προκύπτει ότι το ορθογώνιο με διαστάσεις ![]() έχει την ίδια περίμετρο και το ίδιο εμβαδό.
έχει την ίδια περίμετρο και το ίδιο εμβαδό. 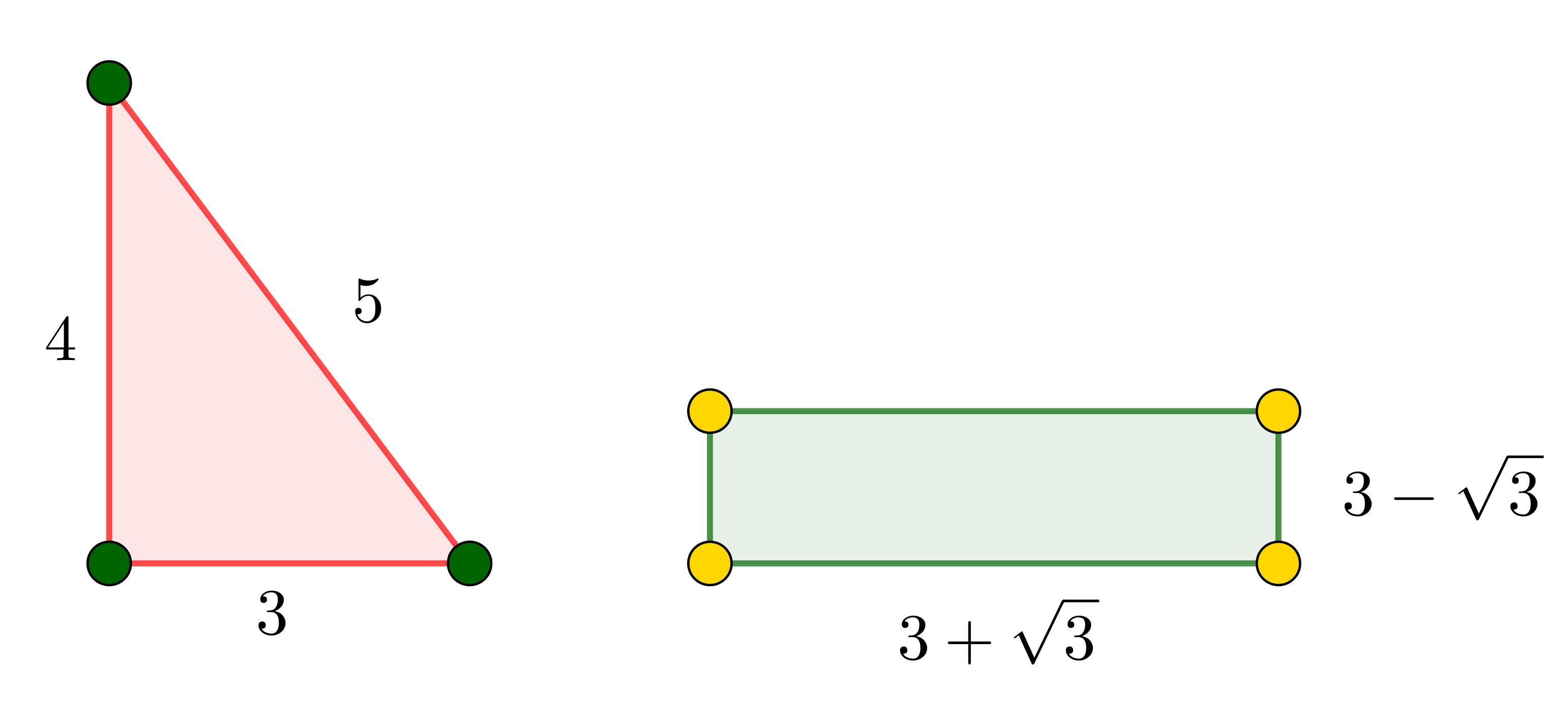
Τρίγωνο με τρίγωνο
Η περίπτωση των τριγώνων, μάλλον, αποτελεί τη βάση του γενικότερου προβλήματος, τουλάχιστον, όταν επιζητείται ίδιος αριθμός πλευρών. Έτσι, αξίζει τον κόπο να εξεταστεί, ιδιαίτερα, αν μπορούν να κατασκευαστούν δύο τρίγωνα με ίση περίμετρο και ίσο εμβαδό.
Ο τύπος ![]() , για το εμβαδό ενός τριγώνου, όπου
, για το εμβαδό ενός τριγώνου, όπου ![]() είναι η ημιπερίμετρός του και
είναι η ημιπερίμετρός του και ![]() η ακτίνα του εγγεγραμμένου του κύκλου, οδηγεί σε ένα αρκετά βοηθητικό συμπέρασμα. Αν θεωρήσουμε ότι δύο διαφορετικά τρίγωνα έχουν ίση περίμετρο και ίσο εμβαδό, τότε, οι εγγεγραμμένοι τους κύκλοι, αναγκαστικά, θα είναι ίσοι.
η ακτίνα του εγγεγραμμένου του κύκλου, οδηγεί σε ένα αρκετά βοηθητικό συμπέρασμα. Αν θεωρήσουμε ότι δύο διαφορετικά τρίγωνα έχουν ίση περίμετρο και ίσο εμβαδό, τότε, οι εγγεγραμμένοι τους κύκλοι, αναγκαστικά, θα είναι ίσοι.
Στην παρακάτω διαδραστική εφαρμογή, έχετε τη δυνανατότητα να επιλέξετε διαφορετικές θέσεις για τα σημεία επαφής του κύκλου με τις πλευρές του περιγεγραμμένου του τριγώνου. Μπορείτε, για έναν δεδομένο εγγεγραμμένο κύκλο, να βρείτε – έστω κατά προσέγγιση – δύο διαφορετικά τρίγωνα με ίσα εμβαδά (οπότε και ίσες περιμέτρους);
Στην προσπάθεια να ανακαλύψουμε, με ακρίβεια, ένα συγκεκριμένο ζεύγος τέτοιων τριγώνων ίσως να είναι προτιμότερο να καταφύγουμε στην ειδική περίπτωση των ισοσκελών τριγώνων.
Συμβολίζοντας, αντίστοιχα, με ![]() τις βάσεις των ισοσκελών τριγώνων και με
τις βάσεις των ισοσκελών τριγώνων και με ![]() τα μήκη των ίσων πλευρών τους,
τα μήκη των ίσων πλευρών τους,
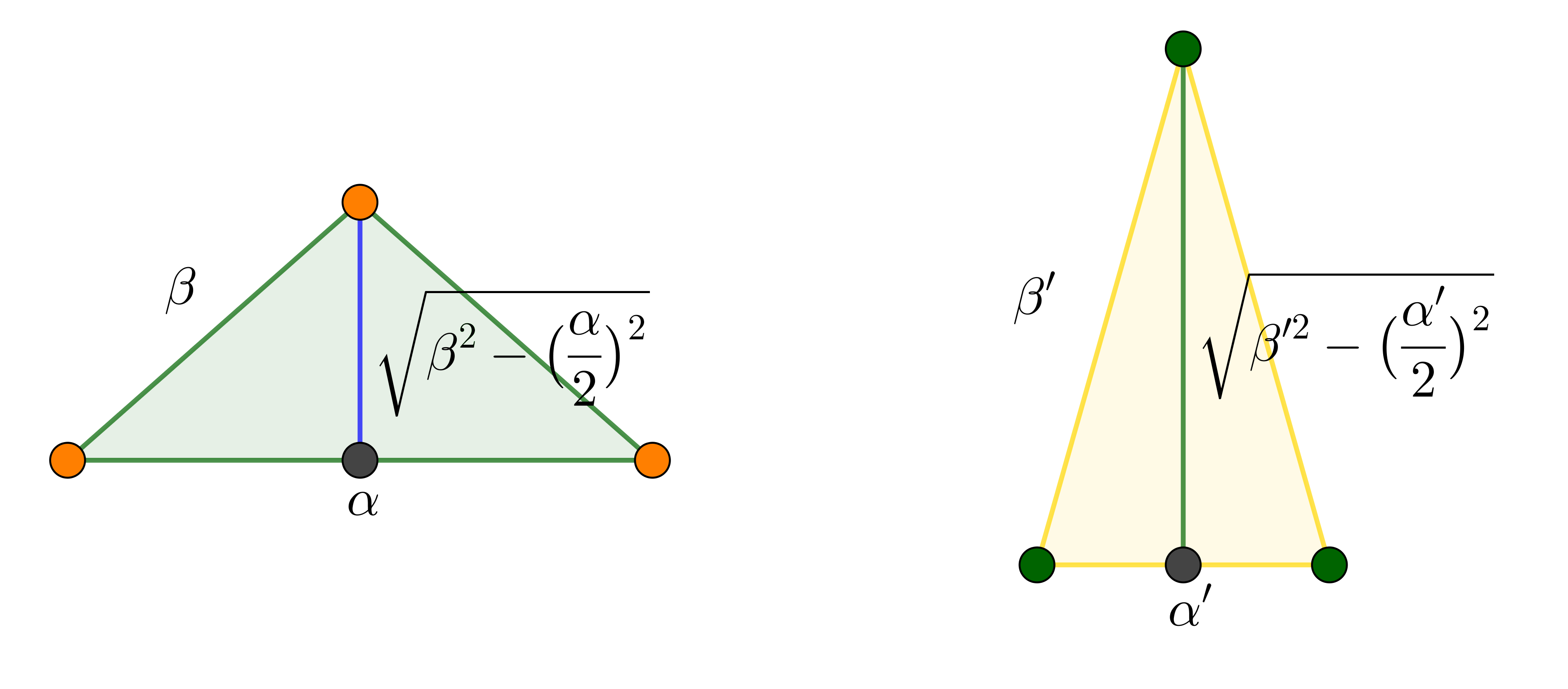 η ισότητα των περιμέτρων τους οδηγεί στη συνθήκη,
η ισότητα των περιμέτρων τους οδηγεί στη συνθήκη, ![]() , ή, ισοδύναμα,
, ή, ισοδύναμα,
(1) ![]()
Επιπλέον, η ισότητα των εμβαδών τους οδηγεί στη σχέση, ![]()
(2) ![]()
(Η ισοδυναμία των δύο τελευταίων αποδεικνύεται με την εφαρμογή της ταυτότητας της διαφοράς τετραγώνων και την αξιοποίηση της σχέσης (1).)
Αντικαθιστώντας στη σχέση (2), όπου (3) ![]() το
το ![]() , από τη σχέση (1), προκύπτει ότι,
, από τη σχέση (1), προκύπτει ότι, ![]()
Υψώνοντας τα δύο μέλη της (3) στο τετράγωνο και επιλύοντας ως προς ![]() , συνάγεται ότι,
, συνάγεται ότι, ![]() , δηλαδή,
, δηλαδή, ![]()
οπότε, ![]()
άρα, ![]()
επομένως, (4) ![]()
Παραδείγματα
Πλέον, μπορούμε, με τη βοήθεια των όσων προηγήθηκαν, να κατασκευάσουμε ορισμένα τρίγωνα που έχουν ίση περίμετρο και ίσο εμβαδό. Πράγματι, για οποιαδήποτε ![]() , λόγω της (4),
, λόγω της (4), ![]() , ενώ, μετά από ορισμένες αλγεβρικές πράξεις,
, ενώ, μετά από ορισμένες αλγεβρικές πράξεις, ![]()
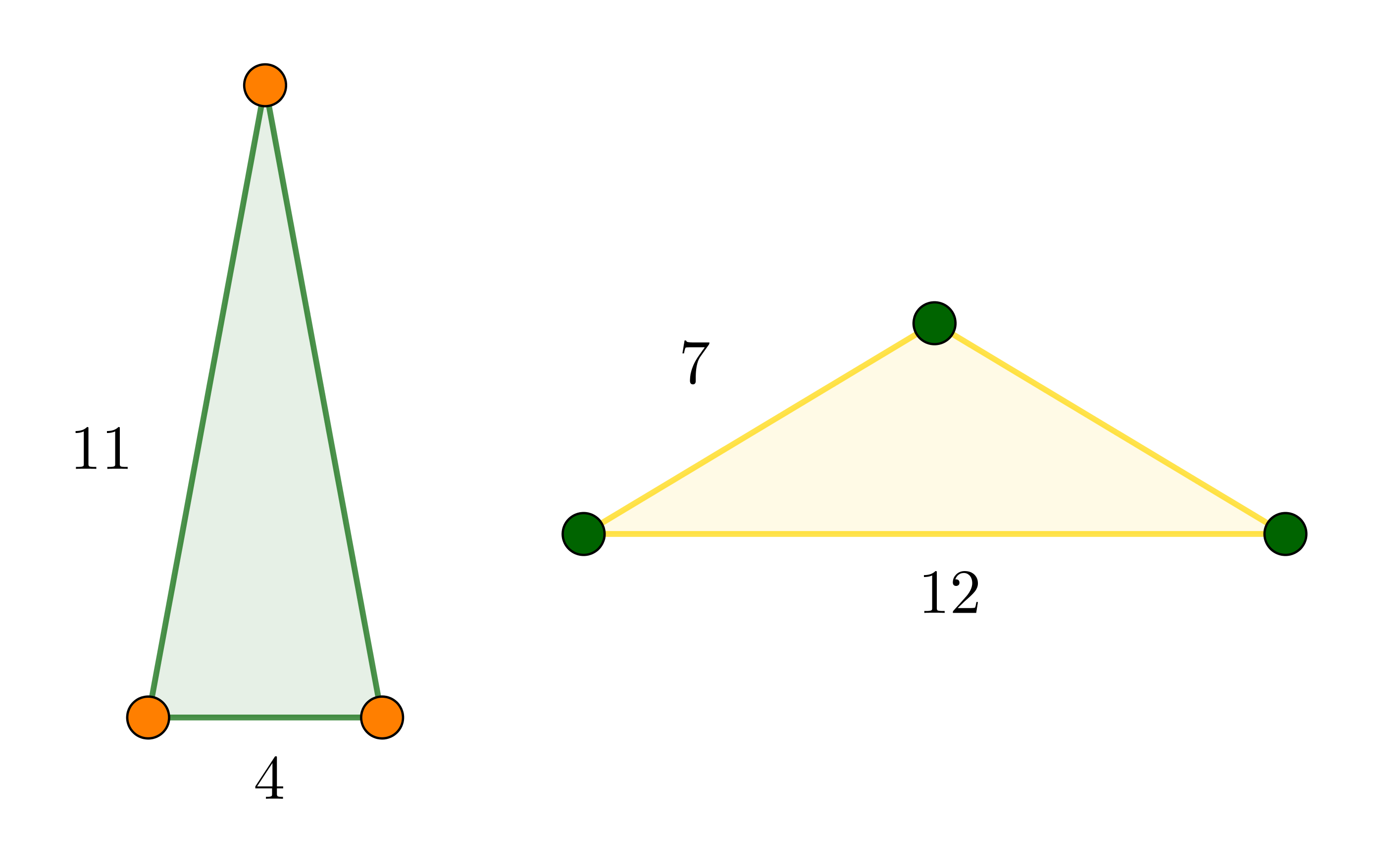
- Από τη σχέση (4), για
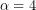 και
και 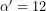 , προκύπτει ότι
, προκύπτει ότι 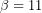 , επομένως, λόγω της (1),
, επομένως, λόγω της (1), 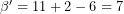 .
.
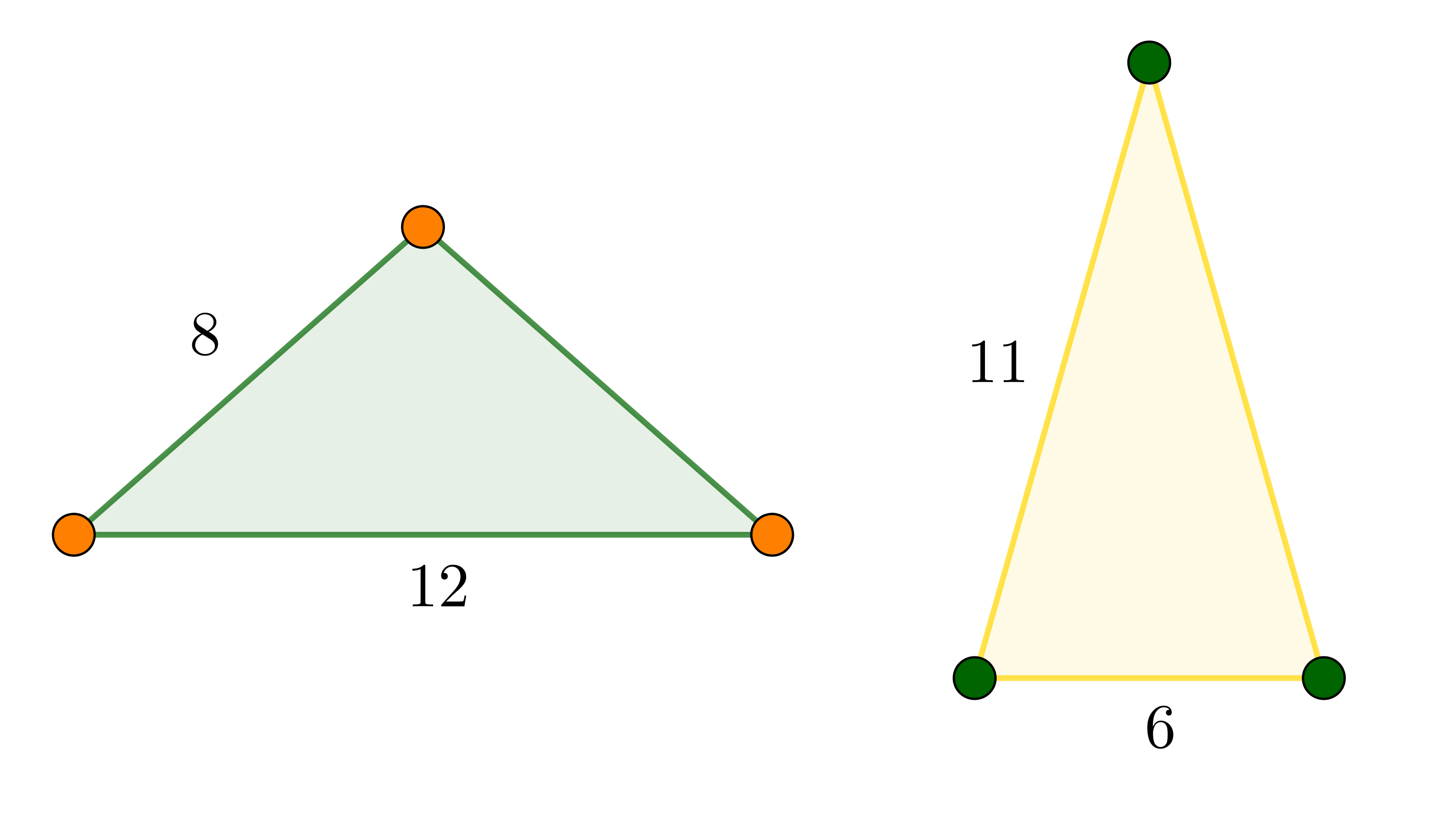
- Από τη σχέση (4), για
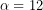 και
και 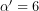 , προκύπτει ότι
, προκύπτει ότι 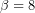 , επομένως, λόγω της (1),
, επομένως, λόγω της (1), 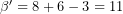 .
.
ν-γωνο με ν-γωνο
Θα μπορούσαμε, παρόμοια, να κατασκευάσουμε δύο τετράπλευρα, πεντάγωνα, εξάγωνα, κ.ο.κ. με ίση περίμετρο και ίσο εμβαδό;
Η απάντηση, κι εδώ, είναι καταφατική. Να προβληματιστείτε, με αυτή τη γενικότερη περίπτωση, έχοντας κατά νου ότι ένα οποιοδήποτε τρίγωνο μπορεί να μετασχηματιστεί σε ένα ισεμβαδικό τετράπλευρο το οποίο μάλιστα έχει την ίδια περίμετρο με αυτό. Η διαδικασία μπορεί να επαναληφθεί, δηλαδή το τετράπλευρο είναι δυνατό να μετασχηματιστεί σε ένα ισοδύναμο πεντάγωνο ίδιας περιμέτρου κ.ο.κ.. Θα μπορούσατε να ολοκληρώσετε τις λεπτομέρειες αυτών των μετασχηματισμών;