Εξισώσεις δεύτερου βαθμού

Μοιραστείτε το!

Εισαγωγή

Για τις εξισώσεις δεύτερου βαθμού, η πρώτη, ιστορικά, προσπάθεια επίλυσής τους εδράζεται, γύρω στο 400 π.Χ., στην αρχαία Βαβυλώνα. Η αποκρυπτογράφηση, από τους σύγχρονους μελετητές, της σφηνοειδούς γραφής των πήλινων πινακίδων της εποχής ανέδειξε τη συμβολή των Βαβυλωνίων στα πρώτα βήματα προς τη γενική μέθοδο.

Ο Αυστριακός Otto Neugebauer, ένας από τους σημαντικότερους ιστορικούς των επιστημών, υπήρξε πρωτοστάτης της έρευνας των Μαθηματικών της Μεσοποταμίας. Στο έργο του, “Οι θετικές επιστήμες στην Αρχαιότητα”, ο Neugebauer μας συστήνει με τις πρώιμες, λεκτικά διατυπωμένες, αλγοριθμικές μεθόδους των Βαβυλωνίων για το ζήτημα των δευτεροβάθμιων εξισώσεων. Κυρίως, οι μέθοδοι αυτές επιστρατεύονταν για να αντιμετωπιστούν πρακτικά γεωμετρικά προβλήματα.

Ενδεικτικά, στη διπλανή εικόνα, παριστάνεται η πήλινη πλάκα, από τη συλλογή του Πανεπιστημίου του Yale, με κωδικό Y.B.C. 4612. Πρόκειται για μαθηματική πήλινη πλάκα της Παλαιοβαβυλωνιακής περιόδου (περίπου 1900–1600 π.Χ.).

Στην πλάκα αναφέρονται 15 προβλήματα εμβαδών, μεταξύ των οποίων και το ακόλουθο:

Η επιφάνεια ενός ορθογωνίου είναι 3600. Πρόσθεσα μήκος και πλάτος και βρήκα 174. Να υπολογιστούν το μήκος και το πλάτος.

Με σημερινή ορολογία, τέτοια προβλήματα οδηγούν στην επίλυση ενός συστήματος, δύο εξισώσεων με δύο αγνώστους, καταλήγοντας στην αναζήτηση των λύσεων μιας δευτεροβάθμιας εξίσωσης.

Βέβαια, στο Βαβυλωνιακό κείμενο, δίνεται μόνο η λύση: Μήκος 150 και πλάτος 24.

Ωστόσο, δε χωρά αμφιβολία ότι οι Βαβυλώνιοι μπορούσαν να εφαρμόσουν κάποια μέθοδο υπολογισμού αυτής της λύσης.

Άλλωστε, στην παρακάτω πήλινη πλάκα, πάλι από τη συλλογή του Πανεπιστημίου του Yale, με κωδικό Y.B.C. 6967, (περίπου 1900 π.Χ.) διατυπώνεται ένα πρόβλημα και η λύση του. Οι λεκτικές περιγραφές, κατά την επίλυση του προβλήματος, αντιστοιχούν στα βήματα της σημερινής μεθόδου της συμπλήρωσης τετραγώνου.

Η διακρίνουσα και οι τύποι των ριζών

Ο Πέρσης φιλόσοφος, μαθηματικός και ποιητής Ομάρ Καγιάμ συνήθιζε να λέει ότι τα συμπεράσματα της Άλγεβρας δεν είναι τίποτε άλλο παρά αποδεδειγμένες γεωμετρικές προτάσεις.

Πραγματικά, η μακροχρόνια προϊστορία, που συνοδεύει τις εξισώσεις δεύτερου βαθμού, συνεχίζεται με τους αρχαίους Έλληνες και τον αμιγώς γεωμετρικό τρόπο επίλυσης. Μια “υβριδική” λύση επανέρχεται, κατά τον μεσαίωνα, χάρη στον Πέρση σοφό Αλ- Κβαρίσμι. Την τωρινή αλγεβρική μορφή τη συναντάμε, μετά το 1600 μ.Χ., χάρη στην καθοριστική συνεισφορά των Γάλλων Viète και Descartes.

Ουσιαστικά, στο πέρασμα των αιώνων, οι γεωμετρικές μέθοδοι της αρχαιότητας εξελίχθηκαν και συμπτύχθηκαν στη σημερινή αλγεβρική μέθοδο επίλυσης των δευτεροβάθμιων εξισώσεων της μορφής,

$\alpha x^2+\beta x+\gamma=0,$

όπου $\alpha\neq0$ .

Πρόκειται για τη γνωστή διαδικασία, που διδάσκεται από το Γυμνάσιο, η οποία χρησιμοποιεί τον τύπο της διακρίνουσας $\Delta=\beta^2-4\alpha\gamma$ και τους τύπους των ριζών $x_{1,2}=\dfrac{-\beta\pm\sqrt{\Delta}}{2\alpha}$ της εξίσωσης.

Όμως, πως προήλθαν και πως αποδεικνύονται αυτοί οι τύποι που, τόσο συχνά, αξιοποιούνται κατά την επίλυση των δευτεροβάθμιων εξισώσεων;

Η απάντηση βρίσκεται σε μια αλγεβρική μέθοδο με γεωμετρική υπόσταση:

Στην περίφημη “συμπλήρωση τετραγώνου”.

Η συμπλήρωση τετραγώνου για τη δευτεροβάθμια εξίσωση

Ας θεωρήσουμε τη δευτεροβάθμια εξίσωση,

$\alpha x^2 + \beta x + \gamma = 0,$

όπου $\alpha\neq 0$ .

Στόχος, κατά την εφαρμογή της συμπλήρωσης τετραγώνου, είναι η προηγούμενη εξίσωση να λάβει τη μορφή,

$(x+\kappa)^2=\lambda,$

για κατάλληλες σταθερές $\kappa$ και $\lambda$ .

Διότι, τότε, θα μπορούσαμε, ευκολότερα, να διερευνήσουμε την επίλυσή της. Πράγματι, για $\lambda<0$ , η προηγούμενη εξίσωση είναι αδύνατη, ενώ, για $\lambda\geq 0$ , έχουμε, $x+\kappa=\pm\sqrt{\lambda}\Leftrightarrow x=-\kappa\pm\sqrt{\lambda}$ .

Η βασική ιδέα της μεθόδου είναι να σχηματίσουμε, κατάλληλα, στο ένα μέλος της εξίσωσης,

$\alpha x^2 + \beta x + \gamma = 0,$

ένα ανάπτυγμα της μορφής $x^2+2\kappa x+\kappa^2$ και στο άλλο μέλος να απομείνει κάτι σταθερό.

Τότε, από τη γνωστή ταυτότητα του τετραγώνου αθροίσματος, θα μπορούσαμε, στο ένα μέλος, να έχουμε ένα τέλειο τετράγωνο, αφού,

$x^2+2\kappa x+\kappa^2=(x+\kappa)^2,$

το οποίο, τελικά, να εξισώνεται με τη σταθερά, έστω $\lambda$ , του άλλου μέλους.

Τα βήματα της μεθόδου

Για τον σκοπό αυτό, ακολουθούμε τα παρακάτω βήματα:

Αρχικά, διαιρούμε όλους τους όρους της εξίσωσης διά $\alpha$ :
$x^2 + \frac{\beta}{\alpha}x + \frac{\gamma}{\alpha} = 0.$
Στη συνέχεια, μεταφέρουμε τον σταθερό όρο της εξίσωσης στο β΄ μέλος:
$x^2 + \frac{\beta}{\alpha}x = - \frac{\gamma}{\alpha} .$
Έπειτα, σχηματίζουμε διπλάσιο γινόμενο στο α΄ μέλος της εξίσωσης:
$x^2 + 2\cdot\frac{\beta}{2\cdot\alpha}x = - \frac{\gamma}{\alpha} .$
Ακολούθως, προσθέτουμε τον ίδιο όρο, στα δύο μέλη της εξίσωσης, για να σχηματιστεί τέλειο τετράγωνο στο α΄ μέλος:
$x^2 + 2\cdot x\cdot\frac{\beta}{2\alpha}+ \Big(\frac{\beta}{2\alpha}\Big)^2= - \frac{\gamma}{\alpha}+ \Big(\frac{\beta}{2\alpha}\Big)^2.$
Πλέον, μπορούμε να σχηματίσουμε το τέλειο τετράγωνο στο α΄ μέλος της εξίσωσης. Ακόμη, είναι βολικό να μετατρέψουμε σε ομώνυμα τα κλάσματα στο β΄ μέλος της εξίσωσης:
$\Big(x + \frac{\beta}{2\alpha}\Big)^2 = - \frac{4\alpha\gamma}{4\alpha^2}+ \frac{\beta^2}{4\alpha^2}.$
Έτσι, αφήνουμε ίδιο το α΄ μέλος και κάνουμε τις πράξεις στο β΄ μέλος της εξίσωσης:
$\Big(x + \frac{\beta}{2\alpha}\Big)^2 = \frac{\beta^2-4\alpha\gamma}{4\alpha^2}.$
Τέλος, διακρίνουμε τις περιπτώσεις:
1. Αν $\beta^2 - 4\alpha\gamma < 0$ , η εξίσωση δεν έχει πραγματικές ρίζες.
2. Αν $\beta^2 - 4\alpha\gamma =0$ , η εξίσωση έχει διπλή ρίζα:
  $x = -\frac{\beta}{2\alpha}.$
3. Αν $\beta^2 - 4\alpha\gamma >0$ , η εξίσωση γράφεται ισοδύναμα,
  $\big(x + \frac{\beta}{2\alpha}\big)^2 = \Big(\frac{\sqrt{\beta^2-4\alpha\gamma}}{2\alpha}\Big)^2$
  ή
  $x + \frac{\beta}{2\alpha} = \pm\frac{\sqrt{\beta^2-4\alpha\gamma}}{2\alpha},$
  που σημαίνει ότι η εξίσωση έχει δύο πραγματικές ρίζες:
  $x = \frac{-\beta \pm \sqrt{\beta^2 - 4\alpha\gamma}}{2\alpha}.$

Η παράσταση

$\Delta = \beta^2 - 4\alpha\gamma,$

λέγεται “διακρίνουσα” της δευτεροβάθμιας εξίσωσης, διότι, προσδιορίζοντας το πρόσημό της, μπορούμε να διακρίνουμε το πλήθος των ριζών της εξίσωσης.

Φύλλο εργασίας στις δευτεροβάθμιες εξισώσεις

Το παρακάτω φύλλο εργασίας αναφέρεται στην ενότητα των δευτεροβάθμιων εξισώσεων. Το φύλλο διαρθρώνεται σε τρεις Δραστηριότητες:

Στη Δραστηριότητα Α, ζητείται να συμπληρώσετε, κατάλληλα, ορισμένα κενά, εφαρμόζοντας τη μέθοδο της συμπλήρωσης τετραγώνου, για να τεκμηριώσετε μόνοι σας τη γνωστή, από το Γυμνάσιο, διαδικασία επίλυσης των δευτεροβάθμιων εξισώσεων. (Μπορείτε να αναζητήσετε τις απαντήσεις στην προηγούμενη παράγραφο αυτού του άρθρου.)
Στη Δραστηριότητα Β, ζητείται μια άσκηση αντιστοίχισης πάνω στα βασικά συμπεράσματα στις δευτεροβάθμιες εξισώσεις.
Στη Δραστηριότητα Γ, ζητείται να εφαρμόσετε αυτούς τους τύπους σε διάφορες δευτεροβάθμιες εξισώσεις συμπληρώνοντας, κατάλληλα, τα κενά.

Η διαδραστική εφαρμογή

Τι θα λέγατε για λίγη εξάσκηση μ’ έναν τρόπο διαδραστικό; Με τη βοήθεια της ακόλουθης εφαρμογής Geogebra, μπορείτε να δοκιμάσετε τις δυνάμεις σας στην επίλυση εξισώσεων β΄ βαθμού. Η εφαρμογή σας καθοδηγεί στα διάφορα στάδια της διαδικασίας:

Εύρεση των συντελεστών της εξίσωσης.
Υπολογισμός της διακρίνουσάς της.
Έλεγχος του πλήθους των λύσεών της.
Εύρεση των λύσεών της (όταν αυτές υπάρχουν).

Επίσης, η εφαρμογή παρέχει τη δυνατότητα ελέγχου των απαντήσεών σας και σας τροφοδοτεί με κατάλληλες βοήθειες.

Καλή ενασχόληση!

Διαδραστικές ασκήσεις στις εξισώσεις δεύτερου βαθμού

Το ακόλουθο διαδραστικό τεστάκι αποτελεί άλλη μια ευκαιρία για βαθύτερη κατανόηση και εμπέδωση των εννοιών της ενότητας των δευτεροβάθμιων εξισώσεων. Να δώσετε προσοχή στα σχόλια και την ανατροφοδότηση των ερωτήσεών του.

Καλή επιτυχία!

Οι τύποι του Viète

Ο François Viète, 1540 – 1603, ήταν Γάλλος Μαθηματικός που θεωρείται πρωτεργάτης και θεμελιωτής της σύγχρονης Άλγεβρας.

Ο Viète εισήγαγε τη συστηματική χρήση γραμμάτων για να δηλώσει τόσο τις γνωστές όσο και τις άγνωστες ποσότητες. Έτσι, καθιέρωσε τη συμβολική άλγεβρα. Στο έργο του, In artem analyticem isagoge (1591), παρουσίασε την «Αναλυτική Τέχνη», όπου οι εξισώσεις αντιμετωπίζονται αλγεβρικά και όχι γεωμετρικά.

Οι επονομαζόμενοι τύποι του Viète, που θα αναλύσουμε, συνδέουν το άθροισμα, $S=x_1+x_2$ , και το γινόμενο, $P=x_1\cdot x_2$ , των ριζών, $x_1,x_2$ , μιας δευτεροβάθμιας εξίσωσης με τους συντελεστές της. Τούτο, για μια δευτεροβάθμια εξίσωση, έχει μεγάλη αξία διότι μπορούν να βρεθούν οι ρίζες της χωρίς την εφαρμογή της μεθόδου της διακρίνουσας.

Άραγε, πως μπορεί να πειραματίστηκε ο Viète πριν καταλήξει στους συγκεκριμένους τύπους συλλαμβάνοντας την αξία τους;

Κατασκευή δευτεροβάθμιας εξίσωσης από τις ρίζες της

Να σκεφτείτε το εξής ερώτημα:

Αν δοθούν δύο αριθμοί, π.χ. οι $2,3$ , τότε, πως θα μπορούσε να βρεθεί μια εξίσωση δεύτερου βαθμού η οποία να έχει τους αριθμούς αυτούς ως λύσεις;

Ίσως, αν αναζητούσατε μια εξίσωση που να είχε μοναδική ρίζα τον έναν από τους δύο παραπάνω αριθμούς, π.χ. τον $x=2$ , να συμπεραίνατε, εύκολα, ότι η πρωτοβάθμια εξίσωση, $x-2=0$ , θα μπορούσε να επιτελέσει αυτόν τον ρόλο.

Παρόμοια, η πρωτοβάθμια εξίσωση $x-3=0$ έχει μοναδική λύση τη $x=3$ .

Πως θα μπορούσαν να συνδυαστούν οι προηγούμενες εξισώσεις για να απαντηθεί το παραπάνω ερώτημα;

Συμφωνείτε ότι η εξίσωση $(x-2)(x-3)=0$ επαληθεύεται τόσο για $x=2$ όσο και για $x=3$ ;

Πράγματι, για $x=2$ , είναι $(2-2)(2-3)=0\cdot (-1)=0$ και για, $x=3$ , είναι $(3-2)(3-3)=1\cdot 0=0$ .

Πολύ περισσότερο, εφαρμόζοντας την επιμεριστική ιδιότητα, η εξίσωση

$(x-2)(x-3)=0,$

γράφεται, $x^2-3x-2x+2\cdot 3=0$ , δηλαδή,

$x^2-(2+3)x+2\cdot 3=0.$

Μήπως παρατηρήσατε την εμφάνιση του αθροίσματος, $2+3$ , όπως και του γινομένου, $2\cdot3$ , των ριζών της εξίσωσης ανάμεσα στους όρους της; Συμβολίζοντας με $S=2+3=5$ (“Sum”) το άθροισμα των ριζών της και με $P=2\cdot3=6$ (“Product”) το γινόμενο των ριζών της, η εξίσωση γράφεται,

$x^2-Sx+P=0.$

Γενικότερα, λοιπόν, ας υποθέσουμε ότι αναζητούμε τη δευτεροβάθμια εξίσωση $\alpha x^2+\beta x+\gamma=0$ , με $\alpha\neq 0$ , η οποία έχει ως ρίζες τους αριθμούς $x_1$ και $x_2$ .

Τότε, ακολουθώντας τα προηγούμενα βήματα, μια τέτοια εξίσωση μπορεί να έχει τη μορφή,

$x^2-Sx+P=0,$

όπου, όπως πριν, $S=x_1+x_2$ και $P=x_1\cdot x_2$ , αποτελούν το άθροισμα και το γινόμενο, αντίστοιχα, των ριζών $x_1$ και $x_2$ .

Η τελική μορφή των τύπων του Viète

Θα δούμε, τώρα, πως συνδέονται το άθροισμα, $S$ , καθώς και το γινόμενο, $P$ , των ριζών μιας δευτεροβάθμιας εξίσωσης, με τους συντελεστές της.

Αρχικά, να παρατηρήσετε ότι η γενική μορφή, $\alpha x^2+\beta x+\gamma=0$ , όπου $\alpha\neq 0$ , μιας δευτεροβάθμιας εξίσωσης, διαιρώντας όλους τους όρους της διά $\alpha$ , ισοδύναμα, γράφεται,

$x^2+\frac{\beta}{\alpha}+\frac{\gamma}{\alpha}=0.$

Ας υποθέσουμε ότι αυτή η εξίσωση έχει ρίζες τις $x_1$ και $x_2$ .

Σύμφωνα με τα προηγούμενα, αφού κι η εξίσωση,

$x^2-Sx+P=0,$

όπου $S=x_1+x_2$ και $P=x_1\cdot x_2$ , έχει ρίζες τις $x_1$ και $x_2$ , εύλογα, έχουμε,

$S=-\frac{\beta}{\alpha}$

και

$P=\frac{\gamma}{\alpha}.$

Παραδείγματα

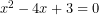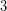Η εξίσωση $x^2-4x+3=0$ έχει $S=-\frac{\beta}{\alpha}=4$ και $P=\frac{\gamma}{\alpha}=3$ . Έτσι, αναζητώντας τις ρίζες της, αρκεί να βρούμε δύο αριθμούς με άθροισμα $4$ και γινόμενο $3$ . Προφανώς, αυτοί οι αριθμοί είναι $x_1=1$ και $x_2=3$ .
Για να βρούμε τη δευτεροβάθμια εξίσωση, με ρίζες τους αριθμούς $x_1=2$ και $x_2=5$ , παρατηρούμε ότι $S=2+5=7$ και $P=2\cdot 5=10$ . Συνεπώς, η ζητούμενη εξίσωση είναι η $x^2-7x+10=0$ .

Διαδραστικές ασκήσεις στους τύπους του Viète

Με το παρακάτω διαδραστικό τεστ, μπορείτε να εξασκηθείτε περισσότερο στους τύπους του Viète και στις εφαρμογές τους. Το τεστ αποτελείται από ποικιλία ερωτήσεων κατανόησης και ασκήσεων εμπέδωσης κλειστού τύπου.

Να αξιοποιήσετε τα σχόλια και την ανατροφοδότηση που παρέχουν οι ερωτήσεις του τεστ.

Καλή επιτυχία!