Τριγωνομετρικός κύκλος

Μοιραστείτε το!

Εισαγωγή

Ο τριγωνομετρικός κύκλος αποτελεί θεμέλιο λίθο για τη βάση των κύριων συμπερασμάτων της Τριγωνομετρίας. Ο συγκεκριμένος κύκλος έχει κέντρο την αρχή $O$ ενός συστήματος αξόνων και ακτίνα $\rho=1$ . Με τη βοήθεια των στοιχείων του τριγωνομετρικού κύκλου, οι τριγωνομετρικοί αριθμοί των γωνιών ανοικοδομούνται σε απλούστερα πλαίσια. Ακόμη, όπως θα δούμε, οι τιμές του συνημιτόνου γωνίας και του ημιτόνου γωνίας, σημειώνονται ως ενδείξεις στους άξονες $x'x$ και $y'y$ , αντίστοιχα. Παρόμοια, μπορούν να σημειωθούν οι τιμές της εφαπτομένης και της συνεφαπτομένης γωνίας σε κατάλληλους άξονες. Έτσι, χάρη στον τριγωνομετρικό κύκλο, αναδεικνύονται, ευκολότερα, διάφορες σχέσεις και συσχετισμοί μεταξύ τριγωνομετρικών αριθμών γωνιών.

Οπότε, ο τριγωνομετρικός κύκλος θα μπορούσε να αποτελέσει ένα εγκόλπιο τριγωνομετρικών τύπων γωνιών. Πράγματι, με τους μηχανισμούς του, χαρτογραφούνται, με τρόπο περίτεχνο, τα μονοπάτια που οδηγούν στις διάφορες τριγωνομετρικές σχέσεις.

Ενδεχομένως, με μια πρώτη ανάγνωση, να μας ξενίζει το γεγονός ότι ένας κύκλος θα αποτελέσει τον οδηγό μας στα άδυτα της Τριγωνομετρίας. Αρχικά, λοιπόν, στο άρθρο αυτό, θα δούμε πως το ορθογώνιο τρίγωνο, που πρωταγωνίστησε στους αρχικούς ορισμούς των τριγωνομετρικών αριθμών, στη Β΄ Γυμνασίου, παραδίδει, με φυσικό τρόπο, τη σκυτάλη, σ’ έναν κατάλληλα εφοδιασμένο κύκλο. Όπως θα διαπιστώσετε, οι γενικότεροι ορισμοί των τριγωνομετρικών αριθμών, με τη βοήθεια των συντεταγμένων ενός σημείου στην τελική πλευρά της γωνίας, που γνωρίσατε στη Γ΄ Γυμνασίου, αποτελούν το μεταβατικό στάδιο. Στη συνέχεια, θα εστιάσουμε στα γνωρίσματα και στα πλεονεκτήματα του τριγωνομετρικού κύκλου.

Τέλος, θα έχετε την ευκαιρία να πειραματιστείτε με το διαδραστικό υλικό του άρθρου. Σε αυτό περιλαμβάνεται μια διαδραστική εφαρμογή Geogebra όπως και διαδραστικά τεστ με ερωτήσεις κατανόησης και ασκήσεις εμπέδωσης.

Aπό το τρίγωνο στον κύκλο

Τριγωνομετρικοί αριθμοί οξείας γωνίας ορθογώνιου τριγώνου

Στη Β΄ Γυμνασίου, στα πρώτα μαθήματα τριγωνομετρίας, γνωρίσατε τους τριγωνομετρικούς αριθμούς οξείας γωνίας. Συγκεκριμένα, το ημίτονο, το συνημίτονο και η εφαπτομένη οξείας γωνίας, $\omega$ , ορίζονται ως κατάλληλοι λόγοι πλευρών ενός ορθογώνιου τριγώνου που έχει την $\omega$ ως γωνία του. Για παράδειγμα, στο παρακάτω σχήμα, για τη γωνία $\omega$ ,

φέρουμε από ένα σημείο, $M$ , της πλευράς της, $OK$ , την κάθετη $MN$ προς την πλευρά της $O\it\Lambda$ .

Τότε, $\sigma\upsilon\nu\,(\omega)=\frac{ON}{OM}$ , $\eta\mu\,(\omega)=\frac{MN}{OM}$ και $\varepsilon\varphi\,(\omega)=\frac{MN}{ON}$ .

(Παρεμπιπτόντως, καθένας από αυτούς τους τριγωνομετρικούς αριθμούς δεν είναι τίποτε άλλο παρά η κοινή τιμή ορισμένων λόγων. Πρόκειται για τα πηλίκα των χρησιμοποιούμενων, αναφορικά με τον τριγωνομετρικό αριθμό, πλευρών των ορθογώνιων τριγώνων, με οξεία γωνία την $\omega$ . Για να καταλάβετε καλύτερα την τελευταία παρατήρηση, αρκεί να επιλέξετε, στην παραπάνω γωνία, $\omega$ , διαφορετικό σημείο $M'$ στην πλευρά της $OK$ . Έπειτα, να φέρετε την κάθετη $M'N'$ στην πλευρά της $O\it\Lambda$ . Τι παρατηρείτε π.χ. για τους λόγους $\frac{ON'}{OM'}$ και $\frac{ON}{OM}$ που, τελικά, εκφράζουν το συνημίτονο της $\omega$ ; Γιατί είναι ίσοι; Βλέπετε ότι η τριγωνομετρία είναι σε άμεση σύνδεση με την ομοιότητα;)

Η περιστροφική κίνηση για μια μεταβαλλόμενη γωνία

Θα διερευνήσουμε, τώρα, τι ακριβώς συμβαίνει καθώς η γωνία, $\omega$ , μεταβάλλεται.

Ας θεωρήσουμε την πιο απλή περίπτωση όπου η πλευρά $O\it\Lambda$ της γωνίας είναι σταθερή και οριζόντια. Επιπλέον, η κατεύθυνσή της, στο επίπεδο της οθόνης, είναι προς τα δεξιά. Αυτή η πλευρά, από εδώ και στο εξής, θα αναφέρεται ως αρχική πλευρά της γωνίας. Σε ό,τι ακολουθεί, η αρχική πλευρά της γωνίας θα παραμένει, σταθερά, σ’ αυτή τη θέση. Η άλλη πλευρά, $OM$ , της γωνίας θα αναφέρεται ως τελική πλευρά. Έτσι, καθώς η τελική πλευρά, $OM$ , της γωνίας $\omega$ μεταβάλλεται, εκκινώντας από την ίδια θέση με την αρχική της πλευρά, $O\it\Lambda$ , οι τιμές της γωνίας $\omega$ αλλάζουν. Συγκεκριμένα, αυτές διατρέχουν το διάστημα $[0^{\circ},360^{\circ}]$ . Μάλιστα, σημειώνοντας, κάθε φορά, ένα σημείο $M$ στην τελική πλευρά της $\omega$ σε σταθερή απόσταση, $\rho=OM$ , από την κορυφή, $O$ , της γωνίας, τότε, το συγκεκριμένο σημείο διαγράφει κυκλική πορεία κέντρου $O$ και ακτίνας $\rho$ .

Το τελευταίο συμπέρασμα για την κυκλική κίνηση του σημείου $M$ , καθώς μεταβάλλεται η γωνία $\omega$ , συνδέεται με το κίνητρο ορισμού τριγωνομετρικών αριθμών γωνιών οι οποίες δεν είναι οξείες. Διότι, για το $M$ , που εκτελεί την κυκλική κίνηση, ένας στόχος, για κάθε τιμή της αντίστοιχης γωνίας, $\omega$ , θα μπορούσε να είναι η εύρεση μιας έκφρασης, για τη θέση του, στο επίπεδο της κίνησής του. Δηλαδή, θα ήταν ιδιαίτερα χρήσιμο να βρίσκονταν τύποι που υπολογίζουν τις συντεταγμένες του $M$ , ως προς οποιασδήποτε τιμή της γωνίας, $\omega$ , χωρίς να είναι απαραίτητο να διακρίνουμε περιπτώσεις για το είδος της γωνίας $\omega$ .

Τριγωνομετρικοί αριθμοί στο επίπεδο συντεταγμένων

Οξεία γωνία

Ας τα πάρουμε τα πράγματα από την αρχή.

Στο παραπάνω σύστημα, για την οξεία γωνία, $\omega$ , αν $\rho=OM$ , τότε, κατά τα γνωστά, από τη Β΄ Γυμνασίου,

$\mathrm{\sigma\upsilon\nu}(\omega)=\frac{ON}{OM}=\frac{x}{\rho},\,\, \mathrm{ \eta\mu}(\omega)=\frac{MN}{OM}=\frac{y}{\rho},$

καθώς και,

$\mathrm{\varepsilon\varphi}(\omega)=\frac{MN}{ON}=\frac{y}{x},\,\, \mathrm{ \sigma\varphi}(\omega)=\frac{ON}{MN}=\frac{x}{y}.$

Συνεπώς, με χρήση π.χ. του ημιτόνου και του συνημιτόνου, οι συντεταγμένες, $(x,y)$ , του σημείου $M$ , θα μπορούσαν, στην προηγούμενη περίπτωση, να υπολογιστούν από τους τύπους ,

$x=\rho\cdot\mathrm{\sigma\upsilon\nu}(\omega)},\,\,y=\rho\cdot\mathrm{\eta\mu}(\omega)}.$

Αμβλεία γωνία

Στη συνέχεια, στο παρακάτω σχήμα, για να προσδιοριστούν, τριγωνομετρικά, οι συντεταγμένες, $(x,y)$ , του $M$ , θα θα αξιοποιηθεί το ορθογώνιο τρίγωνο εξωτερικά της αμβλείας γωνίας $\omega$ .

Αυτό το τρίγωνο περιλαμβάνει την παραπληρωματική γωνία, $\varphi$ , της γωνίας $\omega$ .

Έτσι,

$\mathrm{\sigma\upsilon\nu}(\varphi)=\frac{ON}{OM}=\frac{|x|}{\rho}=-\frac{x}{\rho},\,\, \mathrm{ \eta\mu}(\varphi)=\frac{MN}{OM}=\frac{|y|}{\rho}=\frac{y}{\rho}.$

Συνεπώς,

$x=-\rho\cdot\mathrm{\sigma\upsilon\nu}(\varphi)},\,\,y=\rho\cdot\mathrm{\eta\mu}(\varphi)}.$

Η συγχώνευση των δύο περιπτώσεων

Υπάρχει τρόπος να ενοποιήσει κανείς τις δύο περιπτώσεις και να μην προκύπτουν διαφορετικοί τύποι ανάλογα με το είδος της γωνίας $\omega$ ; Δε θα ήταν χρήσιμο να παρακαμφθεί το βοηθητικό ορθογώνιο τρίγωνο όπου παρεισφρέει μια επιπλέον γωνία, $\varphi$ ;

Μια τέτοια απάντηση δόθηκε στη Γ΄ Γυμνασίου όταν αξιοποιήθηκαν οι τύποι,

$\mathrm{\sigma\upsilon\nu}(\omega)=\frac{x}{\rho},\,\, \mathrm{ \eta\mu}(\omega)=\frac{y}{\rho},$

για τους τριγωνομετρικούς αριθμούς αμβλείας γωνίας ω με τη βοήθεια των συντεταγμένων ενός σημείου, $M$ , στην τελική της πλευρά. Προφανώς, για την περίπτωση της (κυρτής) αμβλείας γωνίας του προηγούμενου σχήματος, ισχύoυν,

$\mathrm{\sigma\upsilon\nu}(\omega)=-\mathrm{\sigma\upsilon\nu}(\varphi),\,\,\mathrm{\eta\mu}(\omega)=\mathrm{\eta\mu}(\varphi).$

Οι γενικότεροι τύποι

Επομένως, φαίνεται ότι, γενικότερα, καθώς $\omega\in[0^{\circ},360^{\circ}]$ , ή αν προτιμάτε, καθώς το $M$ διαγράφει την αντίστοιχη κυκλική πορεία,

μοιάζει εξυπηρετικό, κατά την μελέτη αυτής της επαγόμενης κίνησης, να χρησιμοποιηθούν οι τύποι,

$\mathrm{\sigma\upsilon\nu}(\omega)=\frac{x}{\rho},\,\, \mathrm{ \eta\mu}(\omega)=\frac{y}{\rho},\,\, \mathrm{\varepsilon\varphi}(\omega)=\frac{y}{x},\,\, \mathrm{ \sigma\varphi}(\omega)=\frac{x}{y}.$

Η γενίκευση της έννοιας της γωνίας

Η σύνδεση των μεταβολών της γωνίας $\omega$ με την κυκλική κίνηση του $M$ ανοίγει τον δρόμο για τη γενίκευση της έννοιας της γωνίας. Φυσικά, η κυκλική κίνηση ενός σημείου, μπορεί, θεωρητικά, να συνεχίζεται, αέναα, ή ακόμη και να αλλάζει φορά. Έτσι, αντίστοιχα, η γωνία $\omega$ μπορεί να γίνει μεγαλύτερη από $360^{\circ}$ ή ακόμη και να λάβει αρνητικές τιμές. Μια γωνία μεγαλύτερη από $360^{\circ}$ έχει την έννοια ότι η τελική της πλευρά, προτού καταλήξει στη θέση στην οποία βρίσκεται, έχει διαγράψει κάποιον αριθμό πλήρων περιστροφών. Για παράδειγμα, η γωνία των $390^{\circ}$ έχει, φαινομενικά, το ίδιο “άνοιγμα” με τη γωνία των $30^{\circ}$ . Ωστόσο, η τελική της πλευρά έχει διαγράψει, προτού βρεθεί στη θέση της, μια πλήρη περιστροφή των $360^{\circ}$ . Από την άλλη μεριά, να παρατηρήσετε, στο παρακάτω σχήμα, την αρνητική γωνία $\omega$ .

Αντιλαμβάνεστε την αλλαγή φοράς, από αριστερόστροφη (θετική) σε δεξιόστροφη (αρνητική), κατά την περιστροφή της τελικής της πλευράς, γύρω από το $O$ , καθώς αυτή εκκινεί από τη θέση του θετικού ημιάξονα $Ox$ ;

Προφανώς, οι ισότητες,

όπου $\rho=OM$ , μπορούν να αξιοποιηθούν για να εκφράσουν τους τριγωνομετρικούς αριθμούς τέτοιων γενικευμένων γωνιών. Δηλαδή, οι παραπάνω σχέσεις χρησιμοποιούνται, ενιαία, σε όλες τις περιπτώσεις γωνιών. Άραγε, αφού η ομοιότητα εξασφαλίζει την ανεξαρτησία των τριγωνομετρικών αριθμών από την επιλογή του $M$ , ποια επιλογή, για την ακτίνα $\rho$ , θα απλοποιούσε περισσότερο τους παραπάνω τύπους;

Τα χαρακτηριστικά του τριγωνομετρικού κύκλου

Ο τριγωνομετρικός κύκλος είναι ο κύκλος με κέντρο την αρχή $O(0,0)$ ενός συστήματος αξόνων και ακτίνα $\rho=1$ (μοναδιαίος κύκλος). Θεωρούμε μεταβαλλόμενο σημείο $M(x,y)$ στην περιφέρεια του τριγωνομετρικού κύκλου και την αντίστοιχη γωνία $\omega=x\hat{O}M$ . Πλέον, καθώς το $M$ μπορεί να περιστρέφεται, απεριόριστα, γύρω από το $O$ , κινούμενο προς οποιαδήποτε φορά, η $\omega$ διατρέχει το $\mathbb{R}$ . Εφόσον $\rho=1$ , οι τύποι για το ημίτονο και το συνημίτονο απλοποιούνται ως εξής:

$\mathrm{\sigma\upsilon\nu}(\omega)=x,\,\, \mathrm{ \eta\mu}(\omega)=y.$

Συνεπώς, το συνημίτονο και το ημίτονο μιας γωνίας, με αρχική πλευρά τον θετικό ημιάξονα του συστήματος συντεταγμένων, δεν είναι τίποτε άλλο παρά η τετμημένη και η τεταγμένη, αντίστοιχα, ενός κατάλληλου σημείου: Πρόκειται για το σημείο στο οποίο η τελική πλευρά της γωνίας τέμνει τον μοναδιαίο κύκλο.

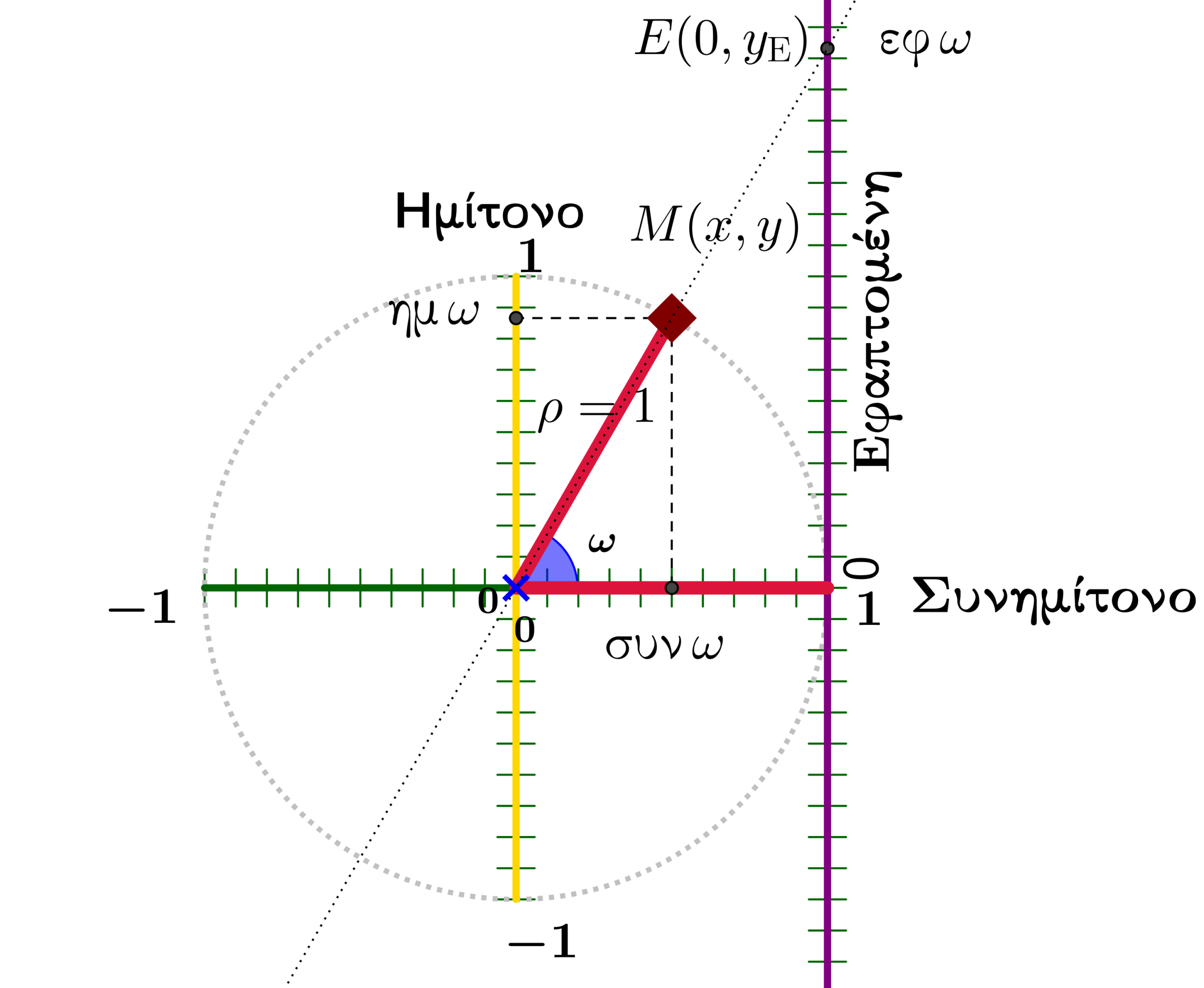
Επίσης, με χρήση της ομοιότητας των δύο σχηματιζόμενων ορθογώνιων τριγώνων, έπεται ότι,

$\mathrm{\varepsilon\varphi}(\omega)=\frac{y}{x}=\frac{y_{E}}{1}=y_{E}.$

Αυτό σημαίνει ότι η εφαπτομένη μιας γωνίας, με αρχική πλευρά τον θετικό ημιάξονα του συστήματος συντεταγμένων, εκφράζει την τεταγμένη του σημείου, $E$ . Το $E$ ορίζεται ως η τομή της ευθείας της τελικής πλευράς της γωνίας με την εφαπτομένη ευθεία του τριγωνομετρικού κύκλου στο σημείο του, $(1,0)$ . Έτσι, η συγκεκριμένη εφαπτομένη ευθεία του κύκλου μπορεί να διαδραματίσει τον ρόλο ενός άξονα εφαπτομένων γωνιών.

Ο τριγωνομετρικός κύκλος και η βαθύτερη κατανόηση του, συνδέονται με τα περισσότερα ζητήματα που μπορεί κανείς να συναντήσει στην Τριγωνομετρία. Η αναγωγή στο πρώτο τεταρτημόριο, η πορεία επίλυσης των τριγωνομετρικών εξισώσεων, καθώς και οι ιδιότητες των τριγωνομετρικών συναρτήσεων αναδεικνύονται από τα ιδιαίτερα χαρακτηριστικά του παραπάνω κύκλου.

Η διαδραστική εφαρμογή

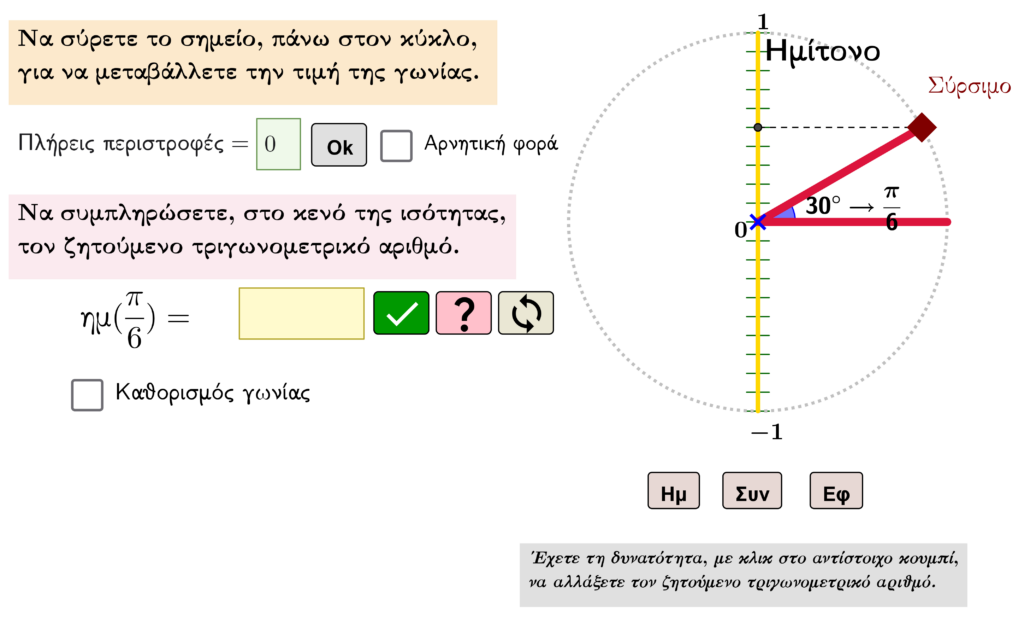
Στην ακόλουθη διαδραστική εφαρμογή μπορείτε να ασκηθείτε με τον τριγωνομετρικό κύκλο και να εμπεδώσετε τα γνωρίσματά του. Η εφαρμογή σας δίνει τη δυνατότητα να πειραματιστείτε με όλες τις περιπτώσεις γωνιών και να αναζητήσετε, κάθε φορά, τους τριγωνομετρικούς αριθμούς της. Το διαδραστικό περιβάλλον της προσφέρεται για εμβάθυνση των εννοιών του τριγωνομετρικού κύκλου όπως και για σχετική ανατροφοδότηση.

Καλή ενασχόληση!

Τριγωνομετρικός κύκλος : Η διαδραστική εφαρμογή

Φόρμα ερωτήσεων: Ο τριγωνομετρικός κύκλος

Η παρακάτω φόρμα αφορά στις βασικές έννοιες του τριγωνομετρικού κύκλου.

Θα μπορούσατε να απαντήσετε στις ερωτήσεις κατανόησης που πραγματεύεται;

Φόρμα ερωτήσεων για διάφορους τριγωνομετρικούς αριθμούς γωνιών στον τριγωνομετρικό κύκλο

Αν έχετε κατανοήσει τις έννοιες του τριγωνομετρικού κύκλου και τη σύνδεσή τους με τους τριγωνομετρικούς αριθμούς γωνιών, τότε, μπορείτε να περάσετε στην επόμενη φόρμα ερωτήσεων.

Εδώ, θα επεξεργαστείτε κάποιες ερωτήσεις κατανόησης αλλά και κάποιες ασκήσεις εμπέδωσης πάνω στον τριγωνομετρικό κύκλο.

Καλή επιτυχία!