Εισαγωγή
Οι ανισώσεις πρώτου βαθμού εγκαινιάζουν το κεφάλαιο των ανισώσεων στην Άλγεβρα της Α΄ Λυκείου. Με τις ανισώσεις, γενικά, θα μπορούσε να διευρυνθεί το φάσμα των προβλημάτων που αντιμετωπίζονται με αλγεβρικές μεθόδους. Άλλωστε, τις περισσότερες φορές, εκφράσεις όπως «μεγαλύτερο / μικρότερο από», «τουλάχιστον / το πολύ» κυριαρχούν στην καθημερινότητά μας.
Τελικά, όπως χαρακτηριστικά έλεγε ο κορυφαίος Γερμανός Μαθηματικός D. Hilbert (1862 – 1943), η ισότητα, μάλλον, παρουσιάζεται ως μια ειδική περίπτωση.
Στις ανισώσεις α΄ βαθμού, ειδικά, η διαδικασία επίλυσης έχει πολλά κοινά με τη γνώριμη διαδικασία επίλυσης των εξισώσεων α΄ βαθμού. Ο χωρισμός γνωστών από αγνώστους όπως και η αναγωγή όμοιων όρων που, συνήθως, ακολουθεί αποτελούν βασικό μέρος των αλγεβρικών χειρισμών. Ιδιαίτερη προσοχή χρήζει η διαίρεση με τον συντελεστή του αγνώστου διότι, από τις ιδιότητες της διάταξης, η φορά της ανίσωσης δεν παραμένει πάντοτε ίδια. Συγκεκριμένα, αν ![]() και
και ![]() , τότε,
, τότε, ![]() , ενώ αν
, ενώ αν ![]() και
και ![]() , τότε,
, τότε, ![]() .
.
Ας επισημανθεί ότι, όταν μια ανίσωση α΄ βαθμού δεν είναι αδύνατη, τότε – αν δε συντρέχουν επιπλέον περιορισμοί – οι λύσεις της είναι άπειρες και όχι μία και μοναδική. Αυτό είναι μια σημαντική διαφορά σε σχέση με τις εξισώσεις α΄ βαθμού. Για παράδειγμα, μια ανισοτική σχέση όπως η ![]() επαληθεύεται από όλους τους αριθμούς
επαληθεύεται από όλους τους αριθμούς ![]() , οι οποίοι ικανοποιούν τη σχέση
, οι οποίοι ικανοποιούν τη σχέση ![]() . Προφανώς, το πλήθος τους είναι άπειρο. Πρόκειται για όλους τους αριθμούς που είναι μεγαλύτεροι του
. Προφανώς, το πλήθος τους είναι άπειρο. Πρόκειται για όλους τους αριθμούς που είναι μεγαλύτεροι του ![]() και βρίσκονται, στην ευθεία των αριθμών, δεξιότερα σε σχέση με το
και βρίσκονται, στην ευθεία των αριθμών, δεξιότερα σε σχέση με το ![]() .
. Από την άλλη μεριά, μπορεί μια ανίσωση να μην έχει καμία λύση, όπως η
Από την άλλη μεριά, μπορεί μια ανίσωση να μην έχει καμία λύση, όπως η ![]() , ή να επαληθεύεται από όλους τους πραγματικούς αριθμούς, όπως η
, ή να επαληθεύεται από όλους τους πραγματικούς αριθμούς, όπως η ![]() .
.
Διερεύνηση για τις ανισώσεις πρώτου βαθμού
Ειδικές περιπτώσεις
Θεωρούμε την ανίσωση ![]() . Κατά την επίλυσή της, μπορούμε να ακολουθήσουμε τα παρακάτω βήματα:
. Κατά την επίλυσή της, μπορούμε να ακολουθήσουμε τα παρακάτω βήματα:
- Αφαιρούμε το
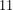 , από τα δύο μέλη της ανίσωσης, οπότε προκύπτει η ανίσωση,
, από τα δύο μέλη της ανίσωσης, οπότε προκύπτει η ανίσωση,  , η οποία γράφεται,
, η οποία γράφεται,  .
. - Διαιρούμε και τα δύο μέλη της ανίσωσης με τον συντελεστή,
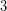 , του αγνώστου
, του αγνώστου  . Έτσι, έχουμε,
. Έτσι, έχουμε,  , άρα οι τιμές,
, άρα οι τιμές,  , με
, με 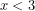 , είναι, τελικά, οι λύσεις της ανίσωσης. Να λάβετε υπόψη ότι η τελευταία ανισοτική σχέση επαληθεύεται και από αριθμούς που δεν είναι ακέραιοι όπως π.χ. το
, είναι, τελικά, οι λύσεις της ανίσωσης. Να λάβετε υπόψη ότι η τελευταία ανισοτική σχέση επαληθεύεται και από αριθμούς που δεν είναι ακέραιοι όπως π.χ. το  , το
, το  , το
, το  κ.ά..
κ.ά.. Παρόμοια, για την ανίσωση
Παρόμοια, για την ανίσωση  , παρατηρούμε ότι, γράφεται, διαδοχικά,
, παρατηρούμε ότι, γράφεται, διαδοχικά,
(Μπορείτε να παρατηρήσετε την αλλαγή φοράς στην ανισότητα κατά τη διαίρεση με τον αρνητικό συντελεστή
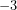 .)
.) 
Κοινές λύσεις
Στην περίπτωση που ενδιαφερόμαστε για τις κοινές λύσεις δύο ανισώσεων, μπορούμε να επιλύσουμε, ξεχωριστά, καθεμία από αυτές και, στη συνέχεια, να προσδιορίσουμε εκείνες τις λύσεις που επαληθεύουν και τις δύο ανισώσεις.
Για παράδειγμα, για να βρούμε τις τιμές του ![]() για τις οποίες ισχύει,
για τις οποίες ισχύει, ![]() , παρατηρούμε ότι,
, παρατηρούμε ότι, 

Συντελεστής αγνώστου μηδέν
Φυσικά, ενώ πάντα μπορούμε να προσθέτουμε στα μέλη μιας ανισότητας τον ίδιο αριθμό, ωστόσο, κατά τη διαίρεση, πρέπει να είναι διασφαλισμένο ότι ο διαιρέτης δεν είναι ίσος με το ![]() . Οπότε, πως μπορούμε να επιλύσουμε ανισώσεις όπου ο συντελεστής του αγνώστου είναι ο αριθμός
. Οπότε, πως μπορούμε να επιλύσουμε ανισώσεις όπου ο συντελεστής του αγνώστου είναι ο αριθμός ![]() ; Ας δούμε δύο παραδείγματα.
; Ας δούμε δύο παραδείγματα.
Έστω, αρχικά, η ανίσωση, ![]() . Για την επίλυσή της, θα ακολουθήσουμε τα παρακάτω βήματα:
. Για την επίλυσή της, θα ακολουθήσουμε τα παρακάτω βήματα:
- Προσθέτουμε το
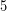 και στα δύο μέλη της ανίσωσης, οπότε προκύπτει η ανίσωση,
και στα δύο μέλη της ανίσωσης, οπότε προκύπτει η ανίσωση,  , δηλαδή, τελικά,
, δηλαδή, τελικά,  .
. - Δε μπορούμε να διαιρέσουμε φυσικά με το
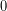 , ωστόσο, δε χρειάζεται να κάνουμε και πολλά περισσότερα. Η ανίσωση είναι, προφανώς, αδύνατη διότι για οποιαδήποτε τιμή του
, ωστόσο, δε χρειάζεται να κάνουμε και πολλά περισσότερα. Η ανίσωση είναι, προφανώς, αδύνατη διότι για οποιαδήποτε τιμή του  το αποτέλεσμα της πράξης
το αποτέλεσμα της πράξης  ισούται με το
ισούται με το 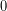 το οποίο, φυσικά, είναι μικρότερο από το
το οποίο, φυσικά, είναι μικρότερο από το 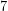 και όχι μεγαλύτερο όπως απαιτεί η συγκεκριμένη ανίσωση.
και όχι μεγαλύτερο όπως απαιτεί η συγκεκριμένη ανίσωση.
Έστω, επίσης, η ανίσωση, ![]() . Για την επίλυσή της, θα ακολουθήσουμε τα παρακάτω βήματα:
. Για την επίλυσή της, θα ακολουθήσουμε τα παρακάτω βήματα:
- Αφαιρούμε το
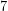 , από τα δύο μέλη της ανίσωσης, οπότε προκύπτει η ανίσωση,
, από τα δύο μέλη της ανίσωσης, οπότε προκύπτει η ανίσωση,  .
. - Πάλι δε μπορούμε να διαιρέσουμε με το
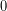 , ωστόσο, αυτό δε σημαίνει απαραίτητα ότι η ανίσωση είναι αδύνατη. Εδώ, ειδικά, όχι μόνο δεν είναι αδύνατη αλλά επαληθεύεται από οποιονδήποτε (πραγματικό) αριθμό. Οποιοσδήποτε αριθμός,
, ωστόσο, αυτό δε σημαίνει απαραίτητα ότι η ανίσωση είναι αδύνατη. Εδώ, ειδικά, όχι μόνο δεν είναι αδύνατη αλλά επαληθεύεται από οποιονδήποτε (πραγματικό) αριθμό. Οποιοσδήποτε αριθμός,  , κι αν πολλαπλασιαστεί επί το
, κι αν πολλαπλασιαστεί επί το 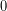 δίνει αποτέλεσμα
δίνει αποτέλεσμα 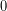 που, προφανώς, είναι μεγαλύτερο από το
που, προφανώς, είναι μεγαλύτερο από το 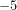 , όπως, δηλαδή, απαιτείται σύμφωνα με το β΄ μέλος της ανίσωσης.
, όπως, δηλαδή, απαιτείται σύμφωνα με το β΄ μέλος της ανίσωσης.
Η γενική περίπτωση για τις ανισώσεις πρώτου βαθμού
Γενικότερα, μια οποιαδήποτε ανίσωση α΄ βαθμού μπορεί να λάβει είτε τη μορφή ![]() είτε τη μορφή
είτε τη μορφή ![]() .
.
Ενδεικτικά, η ανίσωση ![]() , γράφεται, ισοδύναμα,
, γράφεται, ισοδύναμα, ![]()
οπότε είναι της μορφής ![]() , με
, με ![]() και
και ![]() .
.
Θα διερευνήσουμε τη γενική μορφή μιας ανίσωσης πρώτου βαθμού, ![]() , όπου
, όπου ![]() και
και ![]() είναι πραγματικοί αριθμοί. (Η μορφή
είναι πραγματικοί αριθμοί. (Η μορφή ![]() αντιμετωπίζεται παρόμοια.)
αντιμετωπίζεται παρόμοια.)
Αρχικά, παρατηρούμε ότι:
![]()
Έτσι, διακρίνουμε τις περιπτώσεις:
 . Τότε, η ανίσωση γράφεται
. Τότε, η ανίσωση γράφεται  , οπότε έχει άπειρες λύσεις,
, οπότε έχει άπειρες λύσεις,  , όπου
, όπου  .
.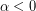 . Τότε, η ανίσωση γράφεται
. Τότε, η ανίσωση γράφεται  , οπότε έχει άπειρες λύσεις,
, οπότε έχει άπειρες λύσεις,  , όπου
, όπου  .
. . Η ανίσωση γράφεται,
. Η ανίσωση γράφεται,  . Έτσι, έχουμε δύο υποπεριπτώσεις:
. Έτσι, έχουμε δύο υποπεριπτώσεις:
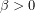 . Η ανίσωση αληθεύει για κάθε
. Η ανίσωση αληθεύει για κάθε  .
. . Η ανίσωση είναι αδύνατη.
. Η ανίσωση είναι αδύνατη.
Στις ακόλουθες διαδραστικές ερωτήσεις – ασκήσεις, μπορείτε να δοκιμάσετε να επιλύσετε ορισμένες ανισώσεις πρώτου βαθμού.
Διαδραστικές ασκήσεις
Ανισώσεις με απόλυτες τιμές (Αλγεβρικά)
Στο άρθρο Απόλυτη τιμή αριθμού και απόσταση είδαμε τον τρόπο όπου, με τη βοήθεια της γεωμετρικής ερμηνείας της απόλυτης τιμής ενός αριθμού και της διαφοράς δύο αριθμών, μπορούν να επιλυθούν ανισώσεις με απόλυτες τιμές. Εδώ, θα προτιμήσουμε έναν περισσότερο αλγεβρικό τρόπο μέσα από την διαπραγμάτευση των παρακάτω παραδειγμάτων.
- Η ανίσωση,
 επαληθεύεται απ’ όλους τους αριθμούς οι οποίοι έχουν απόλυτη τιμή μικρότερη από το
επαληθεύεται απ’ όλους τους αριθμούς οι οποίοι έχουν απόλυτη τιμή μικρότερη από το 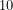 . Οι αριθμοί αυτοί μπορεί να είναι τόσο θετικοί όσο και αρνητικοί. Σίγουρα, θα πρέπει να είναι μικρότεροι από το
. Οι αριθμοί αυτοί μπορεί να είναι τόσο θετικοί όσο και αρνητικοί. Σίγουρα, θα πρέπει να είναι μικρότεροι από το 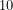 όπως π.χ. οι
όπως π.χ. οι  ,
, 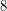 ,
, 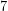 ,
, 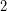 ,
,  ,
, 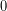 κ.ά.. (Ενδεικτικά,
κ.ά.. (Ενδεικτικά,  .) Συγχρόνως οι αριθμοί που επαληθεύουν την
.) Συγχρόνως οι αριθμοί που επαληθεύουν την  δε μπορεί να είναι μικρότεροι από το
δε μπορεί να είναι μικρότεροι από το  αφού π.χ.
αφού π.χ.  ,
,  κ.ο.κ.. Άρα, τελικά,
κ.ο.κ.. Άρα, τελικά,  που σημαίνει ότι,
που σημαίνει ότι,  .
.
- Η ανίσωση,
 επαληθεύεται, αρχικά, απ’ όλους τους αριθμούς οι οποίοι είναι μεγαλύτεροι από το
επαληθεύεται, αρχικά, απ’ όλους τους αριθμούς οι οποίοι είναι μεγαλύτεροι από το  . Για παράδειγμα,
. Για παράδειγμα,  ,
,  κ.ο.κ.. Ωστόσο, αυτές δεν είναι οι μόνες λύσεις της ανίσωσης
κ.ο.κ.. Ωστόσο, αυτές δεν είναι οι μόνες λύσεις της ανίσωσης  . Πράγματι, οι αριθμοί που είναι μικρότεροι από το
. Πράγματι, οι αριθμοί που είναι μικρότεροι από το  έχουν, επίσης, απόλυτη τιμή μεγαλύτερη από το
έχουν, επίσης, απόλυτη τιμή μεγαλύτερη από το  . Ενδεικτικά,
. Ενδεικτικά,  ,
,  κ.ο.κ.. Επομένως, τελικά,
κ.ο.κ.. Επομένως, τελικά,  .
.
- Η ανίσωση,
 , μπορεί να επιλυθεί άμεσα αφού, θέτοντας
, μπορεί να επιλυθεί άμεσα αφού, θέτοντας  , γράφεται
, γράφεται  , άρα,
, άρα,  , συνεπώς,
, συνεπώς,  . Έτσι,
. Έτσι,
οπότε,![Rendered by QuickLaTeX.com \[-1+1\leq x-1+1\leq1+1,\]](https://dkonas.sites.sch.gr/wp-content/ql-cache/quicklatex.com-7bb1765b19697bf78c78669dc99a0400_l3.png)
 . Επομένως,
. Επομένως, ![Rendered by QuickLaTeX.com x\in[0,2]](https://dkonas.sites.sch.gr/wp-content/ql-cache/quicklatex.com-41098e9f05342d1779a83941b85faa46_l3.png) .
.
- Η ανίσωση,
 , μπορεί να επιλυθεί άμεσα αφού, θέτοντας
, μπορεί να επιλυθεί άμεσα αφού, θέτοντας  , γράφεται
, γράφεται  , άρα,
, άρα,  ή
ή  . Συνεπώς,
. Συνεπώς,  ή
ή  , έτσι,
, έτσι,  ή
ή  . Επομένως,
. Επομένως,  .
.
Στις ακόλουθες διαδραστικές ερωτήσεις – ασκήσεις, μπορείτε να δοκιμάσετε να επιλύσετε ορισμένες ανισώσεις με απόλυτες τιμές.