Εισαγωγή
Ο Νόμος των Συνημιτόνων εκφράζει ένα βασικό συμπέρασμα της Τριγωνομετρίας. Η Τριγωνομετρία αποτελεί έναν θεμελιώδη κλάδο των Μαθηματικών με εφαρμογές που εκτείνονται από τη Γεωμετρία μέχρι την Αστρονομία και τη Φυσική. Οι τριγωνομετρικές μέθοδοι, στα αρχικά στάδια εξέλιξής τους, αποσκοπούσαν, κυρίως, στην εύρεση άγνωστων πλευρών και γωνιών τριγώνων με τη βοήθεια διάφορων γνωστών στοιχείων.
Με τον Νόμο των Συνημιτόνων μπορούμε να εκφράσουμε μια οποιαδήποτε πλευρά τριγώνου με τη βοήθεια των άλλων δύο καθώς και με την περιεχόμενη γωνία αυτών των δύο πλευρών. Πρόκειται για μια ευρύτερη σχέση που γενικεύει το Πυθαγόρειο Θεώρημα το οποίο προϋποθέτει την ύπαρξη ορθής γωνίας. Δηλαδή, ο Νόμος των Συνημιτόνων είναι κατάλληλος για κάθε είδους τρίγωνο, προσφέροντας μια ευέλικτη προσέγγιση στην επίλυση προβλημάτων.
Συγκεκριμένα, σ’ ένα ορθογώνιο τρίγωνο, από το Πυθαγόρειο Θεώρημα, αφαιρώντας από το τετράγωνο της υποτείνουσάς του – της πλευράς απέναντι από την ορθή γωνία – το άθροισμα των τετραγώνων των δύο άλλων κάθετων πλευρών του βρίσκουμε αποτέλεσμα ![]() . Από την άλλη μεριά, σ’ ένα τυχαίο τρίγωνο, όπως θα διαπιστώσουμε από τον Νόμο των Συνημιτόνων, αφαιρώντας από το τετράγωνο μιας πλευράς του το άθροισμα των τετραγώνων των δύο άλλων πλευρών του, βρίσκουμε διαφορά που εξαρτάται από το μέγεθος της γωνίας απέναντι από την πλευρά αυτή.
. Από την άλλη μεριά, σ’ ένα τυχαίο τρίγωνο, όπως θα διαπιστώσουμε από τον Νόμο των Συνημιτόνων, αφαιρώντας από το τετράγωνο μιας πλευράς του το άθροισμα των τετραγώνων των δύο άλλων πλευρών του, βρίσκουμε διαφορά που εξαρτάται από το μέγεθος της γωνίας απέναντι από την πλευρά αυτή.
Σε αυτό το άρθρο, θα επιχειρήσουμε, αρχικά, να αναδείξουμε, περιγραφικά, τη μαθηματική σχέση του Νόμου των Συνημιτόνων. Έπειτα, θα εξερευνήσουμε τις εφαρμογές του και θα δούμε πώς μπορεί να οδηγήσει στις ειδικές περιπτώσεις του Θεωρήματος οξείας και αμβλείας γωνίας. Τέλος, παρατίθενται μια σειρά από διαδραστικές ερωτήσεις κλειστού τύπου τις οποίες μπορείτε να δοκιμάσετε να απαντήσετε.
Περιγραφική προσέγγιση του Νόμου των Συνημιτόνων
Ο μηδέν αδικών ουδενός δείται νόμου. (μτφρ: Όποιος δεν αδικεί, δε χρειάζεται κανένα νόμο.)
Αντιφάνης, 405 – 335 π.Χ., Αρχαίος Κωμωδιογράφος
Να υποθέσετε ότι, σε καθένα απ’ τα ακόλουθα σχήματα, τα τρία τετράγωνα είναι από χρυσό.
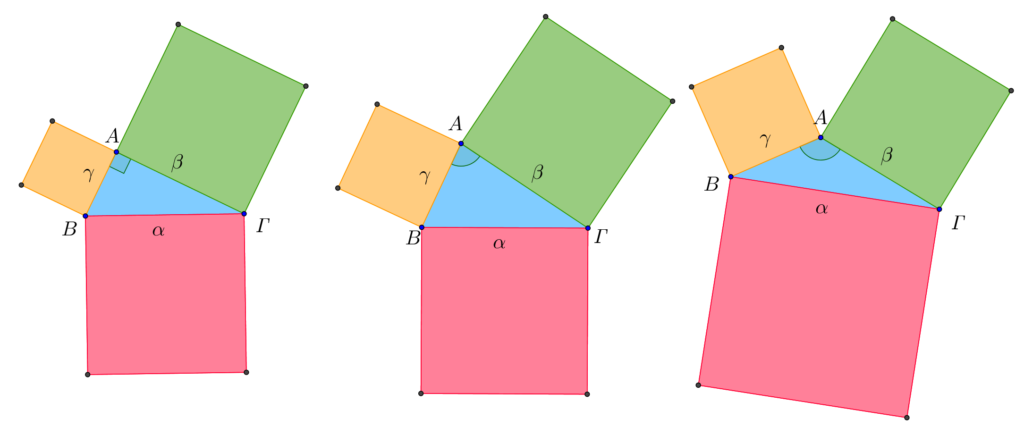
Καθένας από δύο φίλους έχει να επιλέξει, σε κάθε περίπτωση, είτε το τετράγωνο πλευράς ![]() είτε τα άλλα δύο τετράγωνα, μαζί, πλευρών
είτε τα άλλα δύο τετράγωνα, μαζί, πλευρών ![]() και
και ![]() .
.
- Ποια επιλογή θα ήταν περισσότερο συμφέρουσα κάθε φορά;
- Να προσδιορίσετε την «αδικία», ως κατάλληλη διαφορά, που εντοπίζεται, κατά περίπτωση, μεταξύ της μοιρασιάς των δύο φίλων.
- Πότε, σε σχέση με τη γωνία
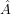 , η προηγούμενη «αδικία» μεγιστοποιείται σε βάρος αυτού που επιλέγει το τετράγωνο πλευράς
, η προηγούμενη «αδικία» μεγιστοποιείται σε βάρος αυτού που επιλέγει το τετράγωνο πλευράς  και πότε σε βάρος αυτού που επιλέγει τα άλλα δύο τετράγωνα, μαζί, πλευρών
και πότε σε βάρος αυτού που επιλέγει τα άλλα δύο τετράγωνα, μαζί, πλευρών 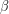 και
και 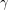 ;
; - Μήπως επιβάλλεται η «θέσπιση» κάποιου «νόμου» για να αντισταθμιστεί αυτή η «αδικία»;
Σε αυτή τη φάση, το μόνο που φανερώνουν, άμεσα, τα παραπάνω σχήματα είναι ότι,
 .
. .
. .
.
Είναι δυνατόν αυτή η διαφορά, μεταξύ του ![]() και του αθροίσματος
και του αθροίσματος ![]() – αυτός είναι ο μαθηματικός όρος για την προηγούμενη “αδικία” – να αποσαφηνιστεί, σε κάθε περίπτωση για τη γωνία
– αυτός είναι ο μαθηματικός όρος για την προηγούμενη “αδικία” – να αποσαφηνιστεί, σε κάθε περίπτωση για τη γωνία ![]() , με τη βοήθεια κατάλληλων στοιχείων του τριγώνου; Όπως θα διαπιστωθεί, σε ένα τέτοιο εγχείρημα, ένας γνωστός τριγωνομετρικός αριθμός θα διαδραματίσει καταλυτικό ρόλο.
, με τη βοήθεια κατάλληλων στοιχείων του τριγώνου; Όπως θα διαπιστωθεί, σε ένα τέτοιο εγχείρημα, ένας γνωστός τριγωνομετρικός αριθμός θα διαδραματίσει καταλυτικό ρόλο.
Ειδικές περιπτώσεις
Πρώτα απ’ όλα, ας εξετάσουμε μια σειρά από ειδικές περιπτώσεις τριγώνων με πλευρές ![]() . Στη συνέχεια, ίσως, να είμαστε σε θέση να διατυπώσουμε τον γενικό κανόνα.
. Στη συνέχεια, ίσως, να είμαστε σε θέση να διατυπώσουμε τον γενικό κανόνα.
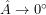 δηλαδή η γωνία
δηλαδή η γωνία 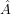 πλησιάζει ολοένα και περισσότερο (τείνει) προς το
πλησιάζει ολοένα και περισσότερο (τείνει) προς το  .
.  Ποια σχέση, οριακά, φαίνεται να ικανοποιούν οι πλευρές
Ποια σχέση, οριακά, φαίνεται να ικανοποιούν οι πλευρές 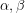 και
και 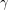 καθώς η γωνία
καθώς η γωνία 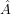 ελαττώνεται, ολοένα και περισσότερο; Μήπως, από την “καταχρηστική” ισότητα,
ελαττώνεται, ολοένα και περισσότερο; Μήπως, από την “καταχρηστική” ισότητα,  , όταν
, όταν  , μπορούμε, υψώνοντας τα μέλη της στο τετράγωνο, να βρούμε την αντίστοιχη σχέση των πλευρών αυτού του “τριγώνου”; Πράγματι, με τη βοήθεια της γνωστής ταυτότητας του τετραγώνου διαφοράς, προκύπτει,
, μπορούμε, υψώνοντας τα μέλη της στο τετράγωνο, να βρούμε την αντίστοιχη σχέση των πλευρών αυτού του “τριγώνου”; Πράγματι, με τη βοήθεια της γνωστής ταυτότητας του τετραγώνου διαφοράς, προκύπτει,  .
.
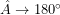 δηλαδή η γωνία
δηλαδή η γωνία 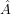 πλησιάζει ολοένα και περισσότερο (τείνει) προς το
πλησιάζει ολοένα και περισσότερο (τείνει) προς το  .
. Ποια σχέση, οριακά, φαίνεται να ικανοποιούν οι πλευρές
Ποια σχέση, οριακά, φαίνεται να ικανοποιούν οι πλευρές 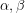 και
και 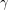 καθώς η γωνία
καθώς η γωνία 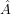 , αυτή τη φορά, αυξάνεται, ολοένα και περισσότερο; Μήπως, από την “καταχρηστική” ισότητα,
, αυτή τη φορά, αυξάνεται, ολοένα και περισσότερο; Μήπως, από την “καταχρηστική” ισότητα,  , όταν
, όταν  , μπορούμε, παρόμοια με την προηγούμενη περίπτωση, υψώνοντας τα μέλη της στο τετράγωνο, να βρούμε την αντίστοιχη σχέση των πλευρών αυτού του “τριγώνου”; Πράγματι, με τη βοήθεια της γνωστής ταυτότητας του τετραγώνου αθροίσματος, προκύπτει,
, μπορούμε, παρόμοια με την προηγούμενη περίπτωση, υψώνοντας τα μέλη της στο τετράγωνο, να βρούμε την αντίστοιχη σχέση των πλευρών αυτού του “τριγώνου”; Πράγματι, με τη βοήθεια της γνωστής ταυτότητας του τετραγώνου αθροίσματος, προκύπτει,  .
. .
. Εδώ, η σχέση είναι η διάσημη ισότητα
Εδώ, η σχέση είναι η διάσημη ισότητα 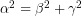 του Πυθαγόρειου Θεωρήματος.
του Πυθαγόρειου Θεωρήματος.
Όπως γίνεται φανερό, από τις παραπάνω ισότητες, η “συμβολή” του όρου ![]() , άλλοτε θετική, άλλοτε αρνητική κι άλλοτε μηδενική, εξαρτάται από την τιμή της γωνίας
, άλλοτε θετική, άλλοτε αρνητική κι άλλοτε μηδενική, εξαρτάται από την τιμή της γωνίας ![]() . Ας συνοψίσουμε,
. Ας συνοψίσουμε,
 . Τότε,
. Τότε,  .
. . Τότε,
. Τότε,  .
. . Τότε,
. Τότε,  .
.
Αντιλαμβάνεστε το γενικότερο συμπέρασμα; Μπορείτε να το εκφράσετε με τη βοήθεια της γωνίας ![]() ;
;
Θα θέλατε, με τη βοήθεια της ακόλουθης διαδραστικής εφαρμογής, να δοκιμάζατε κι άλλες περιπτώσεις για τις τιμές της γωνίας ![]() ;
;
Η διαδραστική εφαρμογή
Τα “παραβατικά” τετράγωνα
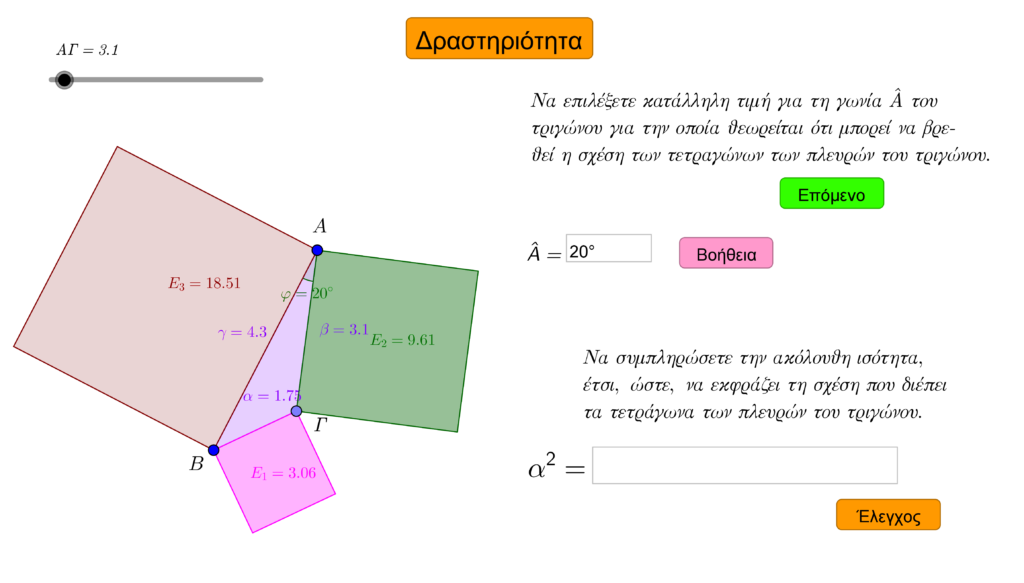
Στόχος της εφαρμογής είναι να αποσαφηνιστεί η σχέση που συνδέει τα τρία τετράγωνα ενός οποιουδήποτε τριγώνου. Γι’ αυτό μπορείτε, στο περιβάλλον της εφαρμογής, να μεταβάλλετε τα κύρια στοιχεία των τριγώνων. Αρχικά, η εφαρμογή διερευνά κάποιες ειδικές «καταχρηστικές» περιπτώσεις τριγώνων. Πρόκειται για τις περιπτώσεις που αναλύθηκαν παραπάνω, δηλαδή όταν,
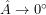 ,
,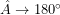 ,
, .
.
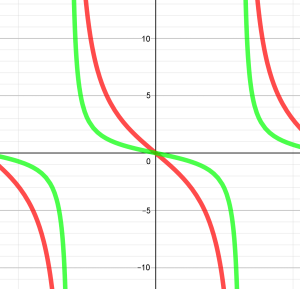
Βέβαια, το κρίσιμο και ουσιαστικότερο ζήτημα είναι η περαιτέρω διερεύνηση. Έτσι, η εφαρμογή παρέχει τη δυνατότητα να εξεταστεί, γραφικά, η μεταβολή της προαναφερόμενης διαφοράς καθώς η γωνία ![]() διατρέχει όλες τις δυνατές τιμές. Ενδεχομένως, το γράφημα που θα προκύψει να μην είναι τελείως άγνωστο σε εσάς.
διατρέχει όλες τις δυνατές τιμές. Ενδεχομένως, το γράφημα που θα προκύψει να μην είναι τελείως άγνωστο σε εσάς.
Μπορείτε, λοιπόν, να καθορίσετε τον νόμο που μπορεί να ελέγξει την “παραβατική” συμπεριφορά των τετραγώνων των πλευρών ενός τυχαίου τριγώνου 🙂 ;
Καλή ενασχόληση!
Η διατύπωση του Νόμου των Συνημιτόνων και των Πορισμάτων του
Όπως καταλάβατε, για ένα τρίγωνο, με πλευρές ![]() ,
,
 ο γενικός τύπος είναι,
ο γενικός τύπος είναι,![]()
Ο παραπάνω τύπος, γνωστός ως Νόμος των Συνημιτόνων, συγχωνεύει δύο πολύ σπουδαία θεωρήματα. Πρόκειται για το θεώρημα οξείας γωνίας και για το θεώρημα αμβλείας γωνίας. Τα τρία συμπεράσματα αποτελούν την ενότητα της γενίκευσης του Πυθαγόρειου Θεωρήματος.
Θεώρημα οξείας γωνίας: Το τετράγωνο πλευράς τριγώνου, που βρίσκεται απέναντι από οξεία γωνία, ισούται με το άθροισμα των τετραγώνων των δύο άλλων πλευρών του ελαττωμένο κατά το διπλάσιο γινόμενο της μιας από αυτές επί την προβολή της άλλης πάνω σ’ αυτήν.
Έτσι, αν στο διπλανό τρίγωνο είναι ![]() , τότε,
, τότε,
![]()
καθώς και,
![]()
Η σύνδεση των δύο παραπάνω τύπων με τον Νόμο των Συνημιτόνων είναι σχετικά απλή. Πράγματι, από το ορθογώνιο τρίγωνο ![]() , είναι
, είναι ![]() και από το ορθογώνιο τρίγωνο
και από το ορθογώνιο τρίγωνο ![]() , είναι,
, είναι, ![]() .
.
Θεώρημα αμβλείας γωνίας: Το τετράγωνο πλευράς τριγώνου, που βρίσκεται απέναντι από αμβλεία γωνία, ισούται με το άθροισμα των τετραγώνων των δύο άλλων πλευρών του αυξημένο κατά το διπλάσιο γινόμενο της μιας από αυτές επί την προβολή της άλλης πάνω σ’ αυτήν.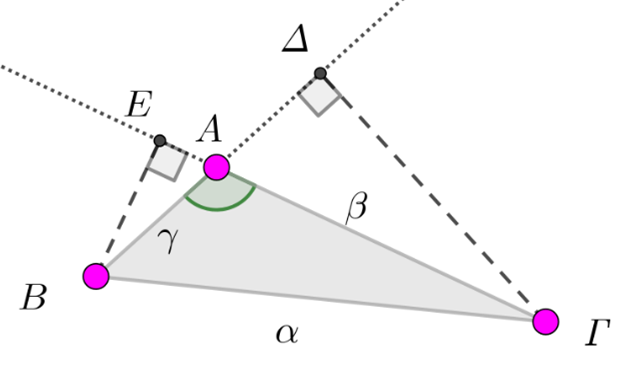
Έτσι, αν στο διπλανό τρίγωνο είναι ![]() , τότε,
, τότε,
![]()
καθώς και,
![]()
Εδώ, η σύνδεση των δύο παραπάνω τύπων με τον Νόμο των Συνημιτόνων είναι λιγότερο προφανής. Ωστόσο, μπορεί, πάλι, να γίνει αξιοποιώντας τα αντίστοιχα ορθογώνια τρίγωνα. Θα χρειαστείτε, επιπλέον, το γνωστό τριγωνομετρικό συμπέρασμα ότι οι παραπληρωματικές γωνίες έχουν αντίθετα συνημίτονα.
Εφαρμογή του νόμου των Συνημιτόνων
Το παρακάτω πρόβλημα μπορεί να αποτελέσει μια εφαρμογή του Νόμου των Συνημιτόνων σε μια πραγματική κατάσταση. Σίγουρα, τέτοιες προεκτάσεις αναδεικνύουν την αξία της Γεωμετρίας στην επίλυση προβλημάτων της καθημερινότητας.
“Διάσωση σε βουνό”
 Ένας σταθμός διάσωσης βρίσκεται στην κορυφή ενός βουνού. Ο σταθμός λαμβάνει σήμα κινδύνου από δύο ορειβάτες που βρίσκονται σε διαφορετικές θέσεις στην πλαγιά.
Ένας σταθμός διάσωσης βρίσκεται στην κορυφή ενός βουνού. Ο σταθμός λαμβάνει σήμα κινδύνου από δύο ορειβάτες που βρίσκονται σε διαφορετικές θέσεις στην πλαγιά.
- Ο πρώτος ορειβάτης, (
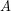 ), βρίσκεται
), βρίσκεται  μακριά από τον σταθμό σε μια κατεύθυνση
μακριά από τον σταθμό σε μια κατεύθυνση  ανατολικά από τον βορρά.
ανατολικά από τον βορρά. - Ο δεύτερος ορειβάτης, (
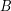 ), βρίσκεται
), βρίσκεται  μακριά από τον σταθμό σε μια κατεύθυνση
μακριά από τον σταθμό σε μια κατεύθυνση  ανατολικά από τον βορρά.
ανατολικά από τον βορρά.
Στον σταθμό επιχειρούν να υπολογίσουν την απόσταση μεταξύ των δύο ορειβατών για να αποφασίσουν αν θα στείλουν μία ή δύο ομάδες διάσωσης.
Μπορείτε να τους βοηθήσετε;
Διαδραστικές ερωτήσεις κατανόησης
Με τις παρακάτω ερωτήσεις καλείστε να ελέγξετε τον βαθμό κατανόησης ορισμένων βασικών συμπερασμάτων αυτής της ενότητας. Όπως μπορείτε να διαπιστώσετε, σε κάθε ερώτηση, δίνονται οι σωστές απαντήσεις οι οποίες συνοδεύονται από κατάλληλα σχόλια. Έτσι, έχετε τη δυνατότητα να επαναλάβετε έννοιες και συμπεράσματα από τη θεωρία με διαδραστικό τρόπο.
Καλή επιτυχία!