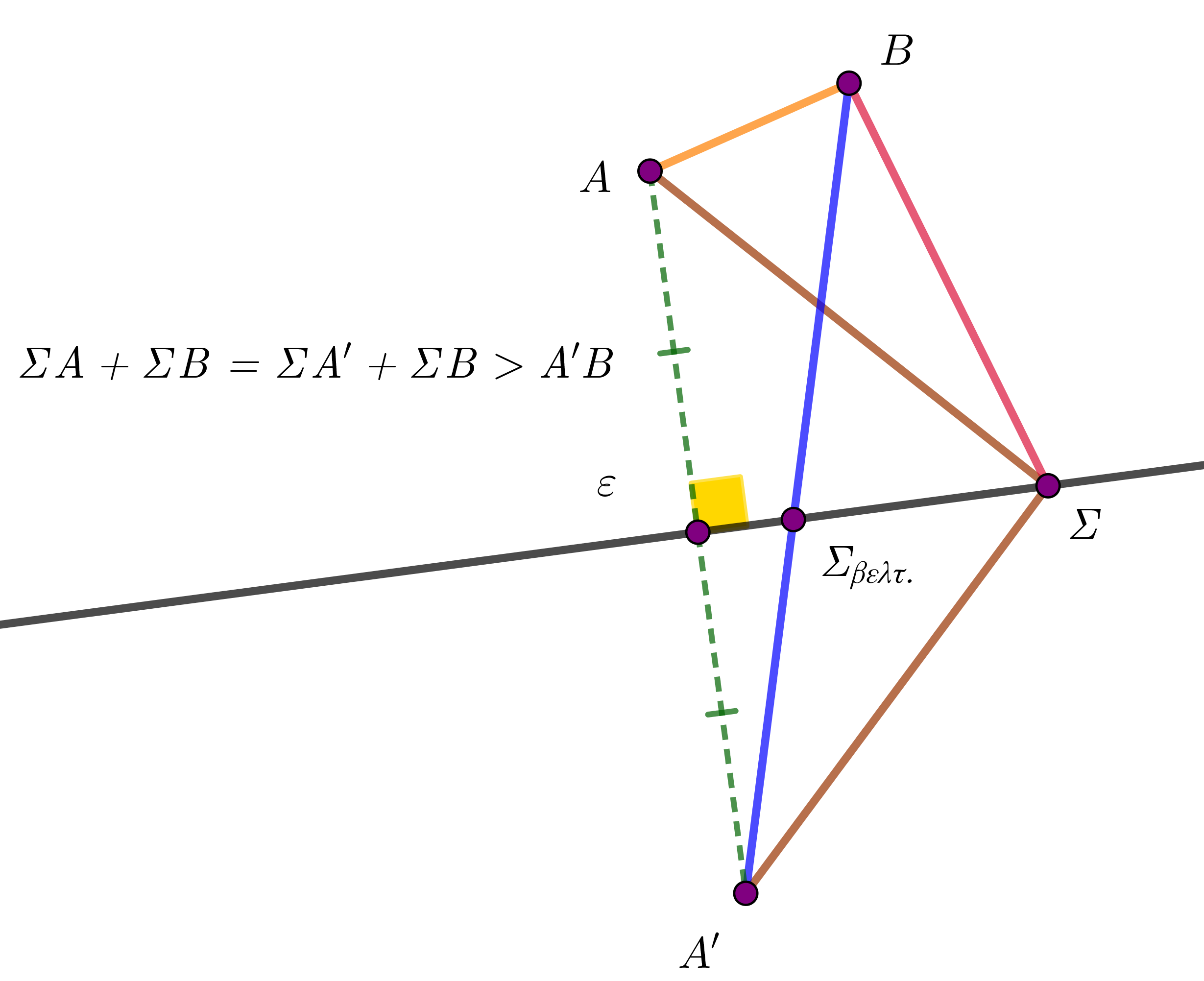Εισαγωγή
Με ποιον τρόπο οι ορθές προβολές των κορυφών ενός οξυγώνιου τριγώνου, στις απέναντι πλευρές του, συνδέονται με ένα πρόβλημα βελτιστοποίησης όπως το περίφημο πρόβλημα του Fagnano;
Στη Γεωμετρία της Α΄Λυκείου, στην ενότητα των ανισοτικών σχέσεων, αποδεικνύονται μια σειρά από συμπεράσματα που σχετίζονται με προβλήματα βελτιστοποίησης. Ας γίνει μια σύντομη ανασκόπηση, για μερικά από αυτά, πριν τη διατύπωση του προβλήματος του Fagnano.
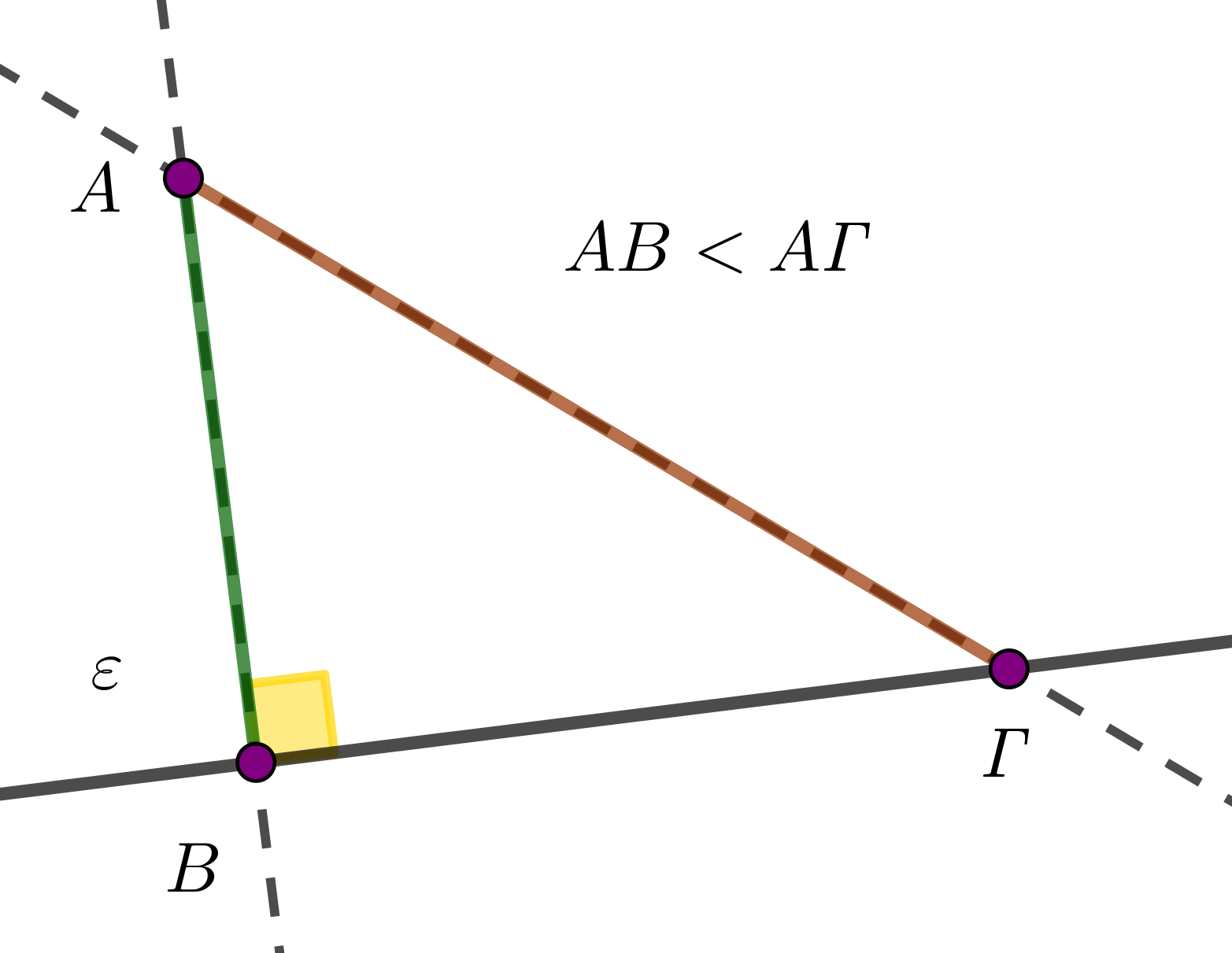
Αρχικά, από σημείο ![]() , που δεν ανήκει σε ευθεία,
, που δεν ανήκει σε ευθεία, ![]() , το κάθετο τμήμα,
, το κάθετο τμήμα, ![]() , προς την ευθεία, είναι μικρότερο από κάθε πλάγιο τμήμα,
, προς την ευθεία, είναι μικρότερο από κάθε πλάγιο τμήμα, ![]() , προς την ευθεία. Αυτό σημαίνει ότι η συντομότερη ευθύγραμμη “διαδρομή” προς μια ευθεία, από ένα σημείο
, προς την ευθεία. Αυτό σημαίνει ότι η συντομότερη ευθύγραμμη “διαδρομή” προς μια ευθεία, από ένα σημείο ![]() , εκτός αυτής, είναι η κάθετη “διαδρομή”,
, εκτός αυτής, είναι η κάθετη “διαδρομή”, ![]() , προς την ευθεία.
, προς την ευθεία.
 Ακόμη, χάρη στην τριγωνική ανισότητα, αποδεικνύεται ότι για δύο σημεία,
Ακόμη, χάρη στην τριγωνική ανισότητα, αποδεικνύεται ότι για δύο σημεία, ![]() και
και ![]() , εκατέρωθεν μιας ευθείας,
, εκατέρωθεν μιας ευθείας, ![]() , το ευθύγραμμο τμήμα,
, το ευθύγραμμο τμήμα, ![]() , που τα ενώνει, έχει το μικρότερο μήκος από οποιαδήποτε τεθλασμένη γραμμή, με άκρα τα δύο σημεία
, που τα ενώνει, έχει το μικρότερο μήκος από οποιαδήποτε τεθλασμένη γραμμή, με άκρα τα δύο σημεία ![]() και
και ![]() , η οποία έχει άλλη μία κορυφή,
, η οποία έχει άλλη μία κορυφή, ![]() , ένα σημείο πάνω στην ευθεία. Αυτό σημαίνει ότι αν θέλαμε να μεταβούμε από το ένα σημείο,
, ένα σημείο πάνω στην ευθεία. Αυτό σημαίνει ότι αν θέλαμε να μεταβούμε από το ένα σημείο, ![]() , προς το άλλο σημείο,
, προς το άλλο σημείο, ![]() , ακολουθώντας τη συντομότερη “διαδρομή”, κατά μήκος ευθύγραμμων τμημάτων, με μια ενδιάμεση “στάση” στην ευθεία, τότε, πρέπει να επιλέξουμε το τμήμα
, ακολουθώντας τη συντομότερη “διαδρομή”, κατά μήκος ευθύγραμμων τμημάτων, με μια ενδιάμεση “στάση” στην ευθεία, τότε, πρέπει να επιλέξουμε το τμήμα ![]() με άκρα τα δύο σημεία.
με άκρα τα δύο σημεία.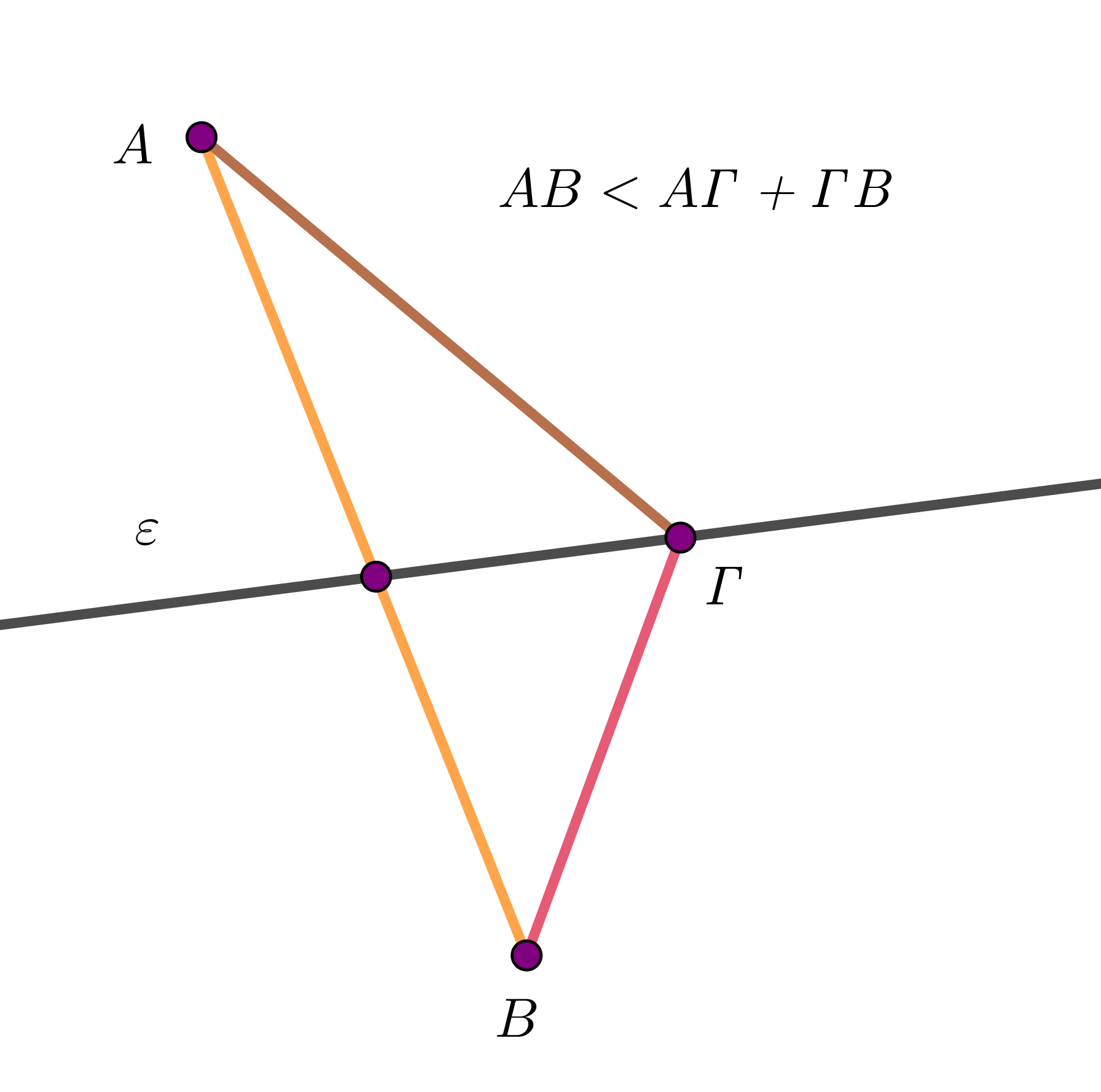 Έστω, τώρα, ότι αναζητείται ένα σημείο,
Έστω, τώρα, ότι αναζητείται ένα σημείο, ![]() , μιας ευθείας
, μιας ευθείας ![]() , του οποίου το άθροισμα των αποστάσεων από δύο άλλα σημεία,
, του οποίου το άθροισμα των αποστάσεων από δύο άλλα σημεία, ![]() και
και ![]() , που βρίσκονται εκτός της ευθείας, αλλά προς το ίδιο μέρος της, γίνεται το ελάχιστο δυνατό. Μήπως η αναζήτηση αυτή θα μπορούσε να οδηγηθεί από την προηγούμενη παρατήρηση;
, που βρίσκονται εκτός της ευθείας, αλλά προς το ίδιο μέρος της, γίνεται το ελάχιστο δυνατό. Μήπως η αναζήτηση αυτή θα μπορούσε να οδηγηθεί από την προηγούμενη παρατήρηση;
Η σχέση που πραγματικά κυβερνάει τα μαθηματικά είναι η ανισότητα. Η ισότητα παρουσιάζεται μόνο ως μια ειδική περίπτωση!
Hilbert , 1862 – 1943
Η διαδραστική εφαρμογή
Στο σημείο αυτό θα ανοίξει μια παρένθεση για ένα διαδραστικό παιχνίδι.
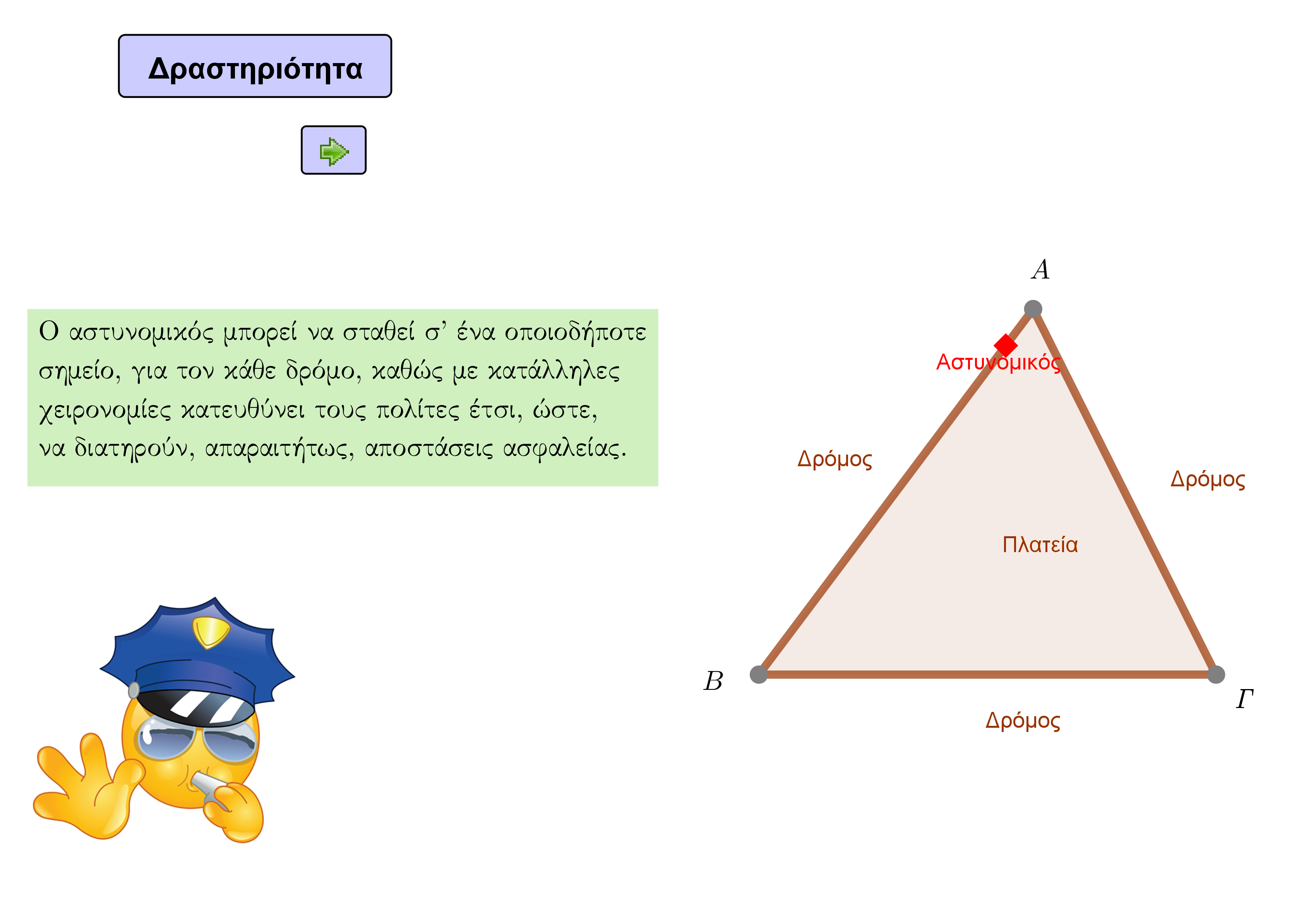
Μια πλατεία, με σχήμα οξυγώνιο τρίγωνο, περικλείεται από τρεις εμπορικούς δρόμους, τους ![]() και
και ![]() . Ένα όργανο της δημοτικής αστυνομίας, το τελευταίο χρονικό διάστημα, έχει αναλάβει τον έλεγχο του συγχρωτισμού των προηγούμενων δρόμων. Ο αστυνομικός μπορεί, για καθένα δρόμο, να σταθεί σ’ ένα οποιοδήποτε σημείο του. Με κατάλληλες χειρονομίες κατευθύνει τους πολίτες έτσι, ώστε, να διατηρούν, απαραιτήτως, αποστάσεις ασφαλείας. Έτσι, ο αστυνομικός μετακινείται, ανά τακτά χρονικά διαστήματα, από δρόμο σε δρόμο, διασχίζοντας ευθύγραμμα την πλατεία, καλύπτοντας, διαδοχικά, και τους τρεις δρόμους. Αναγκαστικά, επαναλαμβάνει, αδιάλειπτα, την προηγούμενη διαδρομή, κατά τη διάρκεια της βάρδιάς του. Μοιάζει, λοιπόν, επιτακτική η ανάγκη να ανακαλύψει τη συντομότερη δυνατή διαδρομή η οποία εξυπηρετεί τον σκοπό της αποστολής του.
. Ένα όργανο της δημοτικής αστυνομίας, το τελευταίο χρονικό διάστημα, έχει αναλάβει τον έλεγχο του συγχρωτισμού των προηγούμενων δρόμων. Ο αστυνομικός μπορεί, για καθένα δρόμο, να σταθεί σ’ ένα οποιοδήποτε σημείο του. Με κατάλληλες χειρονομίες κατευθύνει τους πολίτες έτσι, ώστε, να διατηρούν, απαραιτήτως, αποστάσεις ασφαλείας. Έτσι, ο αστυνομικός μετακινείται, ανά τακτά χρονικά διαστήματα, από δρόμο σε δρόμο, διασχίζοντας ευθύγραμμα την πλατεία, καλύπτοντας, διαδοχικά, και τους τρεις δρόμους. Αναγκαστικά, επαναλαμβάνει, αδιάλειπτα, την προηγούμενη διαδρομή, κατά τη διάρκεια της βάρδιάς του. Μοιάζει, λοιπόν, επιτακτική η ανάγκη να ανακαλύψει τη συντομότερη δυνατή διαδρομή η οποία εξυπηρετεί τον σκοπό της αποστολής του.
Μπορείτε να βοηθήσετε;
Η διατύπωση του προβλήματος του Fagnano
Το 1775, ο Ιταλός μαθηματικός Giovanni Fagnano (31 Ιανουαρίου 1715 – 14 Μαίου 1797), διατύπωσε το ομώνυμο πρόβλημα:
Δίνεται οξυγώνιο τρίγωνο ![]() . Να βρεθεί τρίγωνο
. Να βρεθεί τρίγωνο ![]() το οποίο έχει την ελάχιστη περίμετρο μεταξύ όλων των εγγεγραμμένων τριγώνων του
το οποίο έχει την ελάχιστη περίμετρο μεταξύ όλων των εγγεγραμμένων τριγώνων του ![]() .
.
Ο Fagnano απέδειξε ότι το ζητούμενο τρίγωνο είναι το ορθικό τρίγωνο, δηλαδή αυτό που έχει κορυφές τα ίχνη των υψών του αρχικού τριγώνου στις πλευρές του. Η απόδειξή του στηρίχθηκε σε μεθόδους Απειροστικού Λογισμού. Αυτή που θα παρουσιαστεί στη συνέχεια είναι καθαρά γεωμετρική.
Ενδεχομένως, προηγουμένως, να φανεί χρήσιμο να μελετηθεί η απόδειξη που είχε δοθεί στο άρθρο το σχετικό με το ότι τα ύψη ενός οποιουδήποτε τριγώνου συντρέχουν στο ορθόκεντρό του. Ίσως αυτή η αποδεικτική πορεία να προλειάνει το έδαφος για την αντιμετώπιση του προβλήματος του Fagnano.
Η ανάλυση του προβλήματος του Fagnano και η επίλυσή του
Έστω, λοιπόν, οξυγώνιο τρίγωνο ![]() . Ας υποτεθεί ότι βρέθηκε το ζητούμενο τρίγωνο
. Ας υποτεθεί ότι βρέθηκε το ζητούμενο τρίγωνο ![]() το οποίο έχει την ελάχιστη περίμετρο μεταξύ όλων των εγγεγραμμένων τριγώνων του
το οποίο έχει την ελάχιστη περίμετρο μεταξύ όλων των εγγεγραμμένων τριγώνων του ![]() .
.
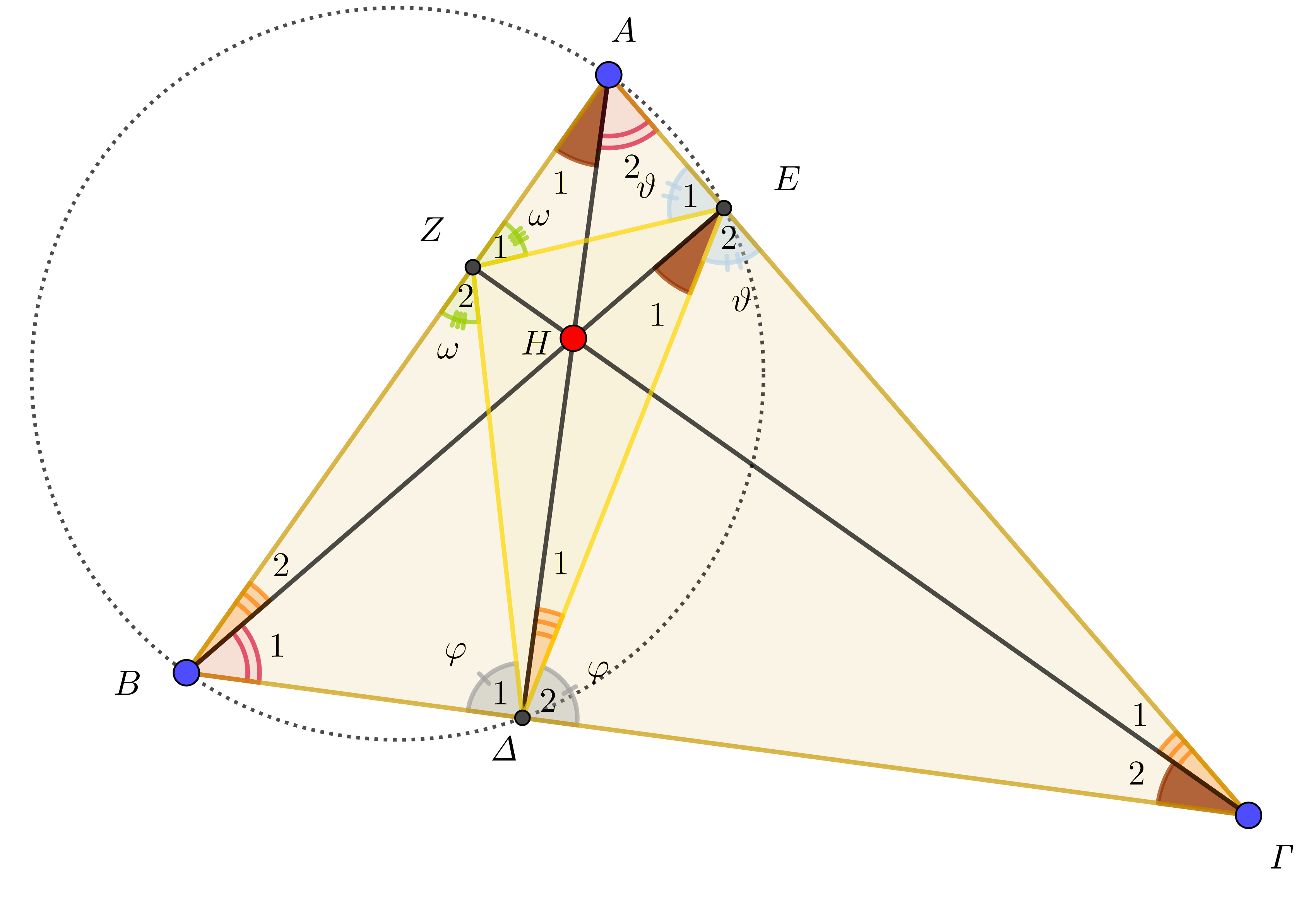 Τότε, το σημείο
Τότε, το σημείο ![]() , θα είναι εκείνο το σημείο του
, θα είναι εκείνο το σημείο του ![]() που έχει το ελάχιστο άθροισμα αποστάσεων από τα
που έχει το ελάχιστο άθροισμα αποστάσεων από τα ![]() και
και ![]() . Από τη στιγμή που το τρίγωνο
. Από τη στιγμή που το τρίγωνο ![]() είναι οξυγώνιο, αυτό σημαίνει ότι οι προβολές των
είναι οξυγώνιο, αυτό σημαίνει ότι οι προβολές των ![]() και
και ![]() θα ανήκουν στη
θα ανήκουν στη ![]() . Σύμφωνα με γνωστό συμπέρασμα, που αναφέρθηκε στο τέλος της εισαγωγής, έπεται ότι,
. Σύμφωνα με γνωστό συμπέρασμα, που αναφέρθηκε στο τέλος της εισαγωγής, έπεται ότι, ![]() . Ομοίως,
. Ομοίως, ![]() και
και ![]() .
.
Έστω, ![]()
Τότε, από το τρίγωνο ![]() , προκύπτει ότι
, προκύπτει ότι ![]() , δηλαδή,
, δηλαδή, ![]()
![]() .
.
Παρατηρώντας το τρίγωνο ![]() , συνάγεται ότι
, συνάγεται ότι ![]() , οπότε,
, οπότε, ![]() . Παρόμοια,
. Παρόμοια, ![]() και
και ![]() . Έτσι, τα τρίγωνα
. Έτσι, τα τρίγωνα ![]() και
και ![]() έχουν τις γωνίες τους ίσες μία προς μία, οπότε είναι όμοια. Άρα, θα έχουν τις αντίστοιχες πλευρές τους ανάλογες. Επομένως,
έχουν τις γωνίες τους ίσες μία προς μία, οπότε είναι όμοια. Άρα, θα έχουν τις αντίστοιχες πλευρές τους ανάλογες. Επομένως, ![]() , δηλαδή,
, δηλαδή, ![]() . Η τελευταία ισότητα, σε συνδυασμό με την ύπαρξη της κοινής γωνίας
. Η τελευταία ισότητα, σε συνδυασμό με την ύπαρξη της κοινής γωνίας ![]() , φανερώνει ότι τα τρίγωνα
, φανερώνει ότι τα τρίγωνα ![]() και
και ![]() είναι όμοια. Συνεπώς,
είναι όμοια. Συνεπώς, ![]() . Ανάλογα,
. Ανάλογα, ![]() και
και ![]() .
.
Θέτουμε, ![]()
Έχουμε,
![Rendered by QuickLaTeX.com \[ \left\{\begin{matrix}x+y=\hat{A}\\ x+z=\hat{\it\Gamma}\\y+z=\hat{B}\end{matrix}\right.,\]](https://dkonas.sites.sch.gr/wp-content/ql-cache/quicklatex.com-5b071d69ac5ab7a78bc97659b4342c66_l3.png)
![Rendered by QuickLaTeX.com \[\left\{\begin{matrix}x=90^\circ-\hat{B}\\y=90^\circ-\hat{\it\Gamma}\\ z=90^\circ-\hat{A}\end{matrix}\right.. \]](https://dkonas.sites.sch.gr/wp-content/ql-cache/quicklatex.com-6ac4379acb0eae3b53cd588eed05e5c5_l3.png)
Το τετράπλευρο ![]() είναι εγγράψιμο σε κύκλο διότι η εξωτερική γωνία της
είναι εγγράψιμο σε κύκλο διότι η εξωτερική γωνία της ![]() είναι ίση με την απέναντι εσωτερική της, δηλαδή την
είναι ίση με την απέναντι εσωτερική της, δηλαδή την ![]() .
.
Έτσι, ![]()
Τελικά, ![]() . Ομοίως,
. Ομοίως, ![]() και
και ![]() , γεγονός που ολοκληρώνει την απόδειξη.
, γεγονός που ολοκληρώνει την απόδειξη.