Κύκλοι τριγώνου - ΜαθηματιΚά

Μοιραστείτε το!

Εισαγωγή

Στη Γεωμετρία, υπάρχουν προβλήματα όπου, για την επίλυσή τους, διαδραματί-ζουν καταλυτικό ρόλο δύο βασικοί κύκλοι τριγώνου. Προτού συζητηθούν οι ορισμοί αυτών των κύκλων, ας εξεταστούν, ενδεικτικά, δύο ερωτήματα:

Πότε τρία μη συνευθειακά σημεία του επιπέδου είναι ομοκυκλικά, δηλαδή, πότε υπάρχει κύκλος που διέρχεται από αυτά τα σημεία; Πως θα μπορούσε να κατασκευαστεί, με ακρίβεια, το κέντρο του και ποια θα είναι η ακτίνα του;
Για τρία μη συνευθειακά σημεία του επιπέδου, είναι γνωστό ότι ορίζεται τρίγωνο. Με ποιο τρόπο θα μπορούσε να γίνει η κατασκευή ενός κύκλου που το εμβαδό του είναι μέγιστο μεταξύ όλων των κύκλων που βρίσκονται στην περιοχή που απαρτίζεται από το εσωτερικό και από το περίγραμμα αυτού του τριγώνου;

Οι κύκλοι τριγώνου, που σχετίζονται με τα προηγούμενα ερωτήματα είναι, αντίστοιχα, ο περιγεγραμμένος και ο εγγεγραμμένος.

Η ανάλυση των ερωτημάτων

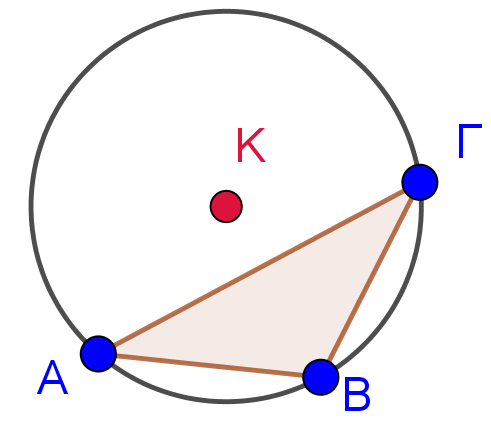
Αναλύοντας το πρώτο ερώτημα, θεωρούμε, σε μια αντίστροφη διεργασία, τρία σημεία $A$ , $B$ και $\it\Gamma$ του κύκλου $(K)$ . Να θυμηθείτε ότι από την χαρακτηριστική ιδιότητα των σημείων του κύκλου τα σημεία $A$ , $B$ και $\it\Gamma$ ισαπέχουν από το $K$ . Έτσι, το $K$ , αναγκαστικά, βρίσκεται στις μεσοκαθέτους των τμημάτων $AB$ και $B\it\Gamma$ .

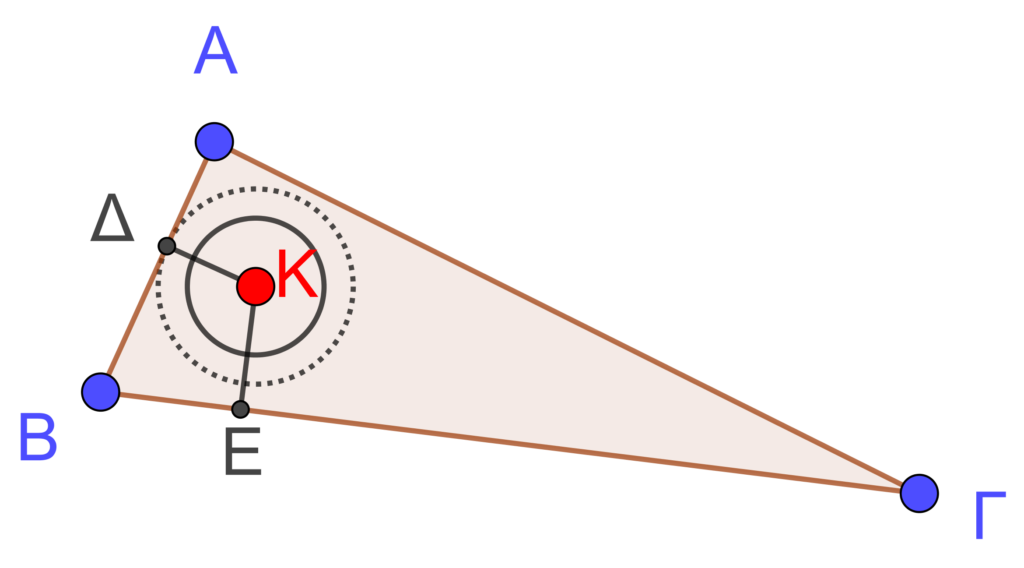Για την ανάλυση του δεύτερου ερωτήματος, παρόμοια με προηγουμένως, θεωρούμε κύκλο $(K)$ στο εσωτερικό του τριγώνου $\overset{\triangle }{AB\it\Gamma}$ . Σύμφωνα με το ζητούμενο του προβλήματος, θα μπορούσαμε να “μεγαλώσουμε” τον κύκλο $(K)$ , αυξάνοντας την ακτίνα του, έτσι, ώστε να εφάπτεται σε μια πλευρά του τριγώνου, έστω την $AB$ στο σημείο $\it\Delta$ .

Τότε, αν υποτεθεί ότι η απόσταση $KE$ του $K$ από τη $B\it\Gamma$ είναι διαφορετική από την απόσταση $K\it\Delta$ του $K$ από την $AB$ , αναγκαστικά, $KE>K\it\Delta$ . (Σε διαφορετική περίπτωση, ο κύκλος θα έτεμνε σε δύο σημεία τη $B\it\Gamma$ .) Παρόμοιο συμπέρασμα προκύπτει και για την απόσταση του $K$ από την τρίτη πλευρά.

Ίσως, πλέον, τουλάχιστον, διαισθητικά, να έγινε αντιληπτό το γιατί ο κύκλος μπορεί να “μεγαλώσει” περαιτέρω μετατοπίζοντας το κέντρο του $K$ στη θέση όπου αυτές οι αποστάσεις ταυτίζονται. Προφανώς, η ακτίνα του είναι η κοινή τιμή αυτών των αποστάσεων και ο κύκλος εγγράφεται στο τρίγωνο με την έννοια ότι οι πλευρές του εφάπτονται σ’ αυτό.

Η διαδραστική εφαρμογή

Στην παρακάτω διαδραστική εφαρμογή, ένας μηχανικός, μάλλον, θα χρειαστεί την καθοδήγησή σας για να ολοκληρώσει το σχέδιό του.

Όπως θα διαπιστώσετε, θα πρέπει να απαντήσει στα ερωτήματα της εισαγωγής. Τρόπον τινά θα χρειαστεί να σχεδιάσει τον περιγεγραμμένο και τον εγγεγραμμένο κύκλο τριγώνων. Βέβαια, αυτό προϋποθέτει την εύρεση των αντίστοιχων κέντρων τους: του περίκεντρου και το έγκεντρου.
Μπορείτε να βοηθήσετε;