Εισαγωγή
Πως να διδάξει κανείς, στο Γυμνάσιο, το άρρητο της τετραγωνικής ρίζας του 2; Σίγουρα, είναι ένα εγχείρημα με ιδιαίτερες δυσκολίες για οποιαδήποτε τάξη. Ενδεχομένως, τα εμπόδια να πολλαπλασιάζονται στις μικρότερες τάξεις, τουλάχιστον, ως προς το επίπεδο κατανόησης και εμβάθυνσης του θέματος.
Το άρρητο της τετραγωνικής ρίζας του 2, ένα ζήτημα που προκάλεσε τριγμούς στα Μαθηματικά και τριβές μεταξύ των σοφών της αρχαιότητας, ίσως να δικαιώνει, διαχρονικά, τον ιδιαίτερο χαρακτηρισμό του (“άρρητο” = αυτό που “δε λέγεται” / “εκφράζεται”) ως ένα θέμα ταμπού και απλησίαστο 😛 .
Ας επιχειρήσουμε να ξετυλίξουμε το κουβάρι της αρρητότητας, ξεπερνώντας τις όποιες μαθηματικές προκαταλήψεις …
Μέτρηση
Είναι σίγουρο ότι είστε εξοικειωμένοι με τη διαδικασία της μέτρησης ευθύγραμμων τμημάτων. Θα έχετε καταλάβει ότι δε μπορεί να είναι πάντοτε ακριβής. Αντίθετα, τις περισσότερες φορές έχει προσεγγιστικό χαρακτήρα. Άραγε, γιατί συμβαίνει αυτό;
Θα έλεγε κανείς ότι το ευθύγραμμο τμήμα δεν ευθύνεται σε τίποτα. Παραμένει «αμέτοχο» και «παθητικό» καθ’ όλη τη διαδικασία, «αναμένοντας» τη μέτρησή του.
Από την άλλη πλευρά, το ανθρώπινο χέρι και το ανθρώπινο μάτι δε μπορούν να συνεργαστούν πάντοτε αρμονικά. Ακόμη, το ίδιο το όργανο μέτρησης, που χρησιμοποιείται, δεν έχει απεριόριστες δυνατότητες. Όπως γνωρίζετε, σ’ ένα συνηθισμένο υποδεκάμετρο, οι υποδιαιρέσεις του είναι συγκεκριμένες: δεκατόμετρα (δέκατα), εκατοστόμετρα (εκατοστά), χιλιοστόμετρα (χιλιοστά).
Ηλεκτρονικό υποδεκάμετρο
Οι παραπάνω αδυναμίες ξεπερνιούνται σε σημαντικό βαθμό με τη βοήθεια ενός «ηλεκτρονικού υποδεκάμετρου». Όπως θα διαπιστώσετε, μάς παρέχει πολύ μεγαλύτερη ακρίβεια από ένα συνηθισμένο υποδεκάμετρο. Επίσης, η πιθανότητα ανθρώπινου σφάλματος ελαττώνεται αρκετά.
Στο ακόλουθο γραφικό, καλείστε να μετρήσετε, επακριβώς, τρία διαφορετικά ευθύγραμμα τμήματα, με ένα τέτοιο ηλεκτρονικό υποδεκάμετρο. Αρκεί να χρησιμοποιήσετε, επαναληπτικά, το εργαλείο του μεγεθυντικού φακού, κατάλληλο αριθμό επαναλήψεων, διαφορετικό, ίσως, για κάθε ευθύγραμμο τμήμα.
Ακριβής μέτρηση
Τι σημαίνει, λοιπόν, «ακριβής μέτρηση» για το μήκος ενός ευθύγραμμου τμήματος;
Όπως έγινε αντιληπτό, αρκεί να τοποθετηθεί το όργανο μέτρησης – στην προκειμένη περίπτωση το ηλεκτρονικό υποδεκάμετρο – έτσι, ώστε, το 
να συμπέσει με το ένα άκρο του ευθύγραμμου τμήματος και έπειτα να βρεθεί, μεγεθύνοντας αν χρειαστεί, η ένδειξη που αντιστοιχεί στο άλλο άκρο του τμήματος.
Για μια στιγμή, είναι λογικό να υποτεθεί ότι κάτι τέτοιο θα μπορούσε να γίνει σε οποιοδήποτε ευθύγραμμο τμήμα. Όμως, προκύπτουν αναπόφευκτα ορισμένα ερωτήματα:
Μπορούμε να μεγεθύνουμε όσες φορές κι αν χρειαστεί, ή ακόμη και η χρήση ενός ηλεκτρονικού υποδεκάμετρου έχει τους δικούς της περιορισμούς;
Άρα, μήπως μπορούμε πάντοτε να βρίσκουμε τμήματα, που το μήκος τους «δραπετεύει» από τη διαδικασία της ακριβής μέτρησης;
Τελικά, αυτό να οφείλεται μόνο στην ανθρώπινη αδυναμία να κατασκευαστεί και να χρησιμοποιηθεί στην εντέλεια ένα ακριβές όργανο μέτρησης;
Κι όμως, όσο παράλογο κι αν ακούγεται, ακόμη κι αν υποτεθεί ότι π.χ. αυτό το ηλεκτρονικό υποδεκάμετρο μπορεί να χρησιμοποιηθεί με τρόπο που να αξιοποιεί τη δυνατότητα της μεγέθυνσης απεριόριστα, πάλι δε θα μπορεί να μετρηθεί επακριβώς το μήκος οποιουδήποτε ευθύγραμμου τμήματος.
Αυτό συμβαίνει διότι στις ενδείξεις ενός υποδεκάμετρου βρίσκονται κλασματικοί (ρητοί) αριθμοί.
Αρρητότητα
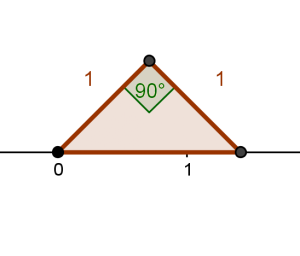
Για παράδειγμα, στο ακόλουθο γραφικό, παριστάνεται ένα ορθογώνιο και ισοσκελές τρίγωνο με κάθετες πλευρές ίσες με 
.
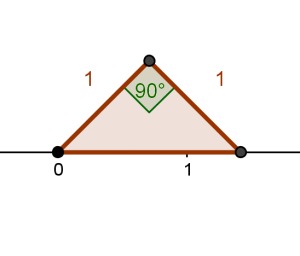Αλληλεπιδρώντας μαζί του, μπορείτε να διαπιστώσετε, τουλάχιστον, ως ένα βαθμό, ότι δε μπορείτε να μετρήσετε το μήκος της υποτείνουσάς του, χρησιμοποιώντας τις υποδιαιρέσεις του υποδεκάμετρου. Μάλιστα, ακόμη κι αν υπήρχε η δυνατότητα να μεγεθύνετε περαιτέρω το προηγούμενο γραφικό, πάλι δε θα αντιστοιχιζόταν κανείς κλασματικός αριθμός στο μήκος της.
Οι πρώτοι που ανακάλυψαν αυτήν την «αδυναμία» πρέπει να ήταν οι Πυθαγόρειοι. Θεωρείται, μάλιστα, ότι απέδειξαν ότι το μήκος της υποτείνουσας αυτού του ορθογώνιου τριγώνου δεν είναι κλασματικός (ρητός) αριθμός. Μ’ άλλα λόγια, ότι ο αριθμός 
δεν είναι κλασματικός (ρητός). Επειδή ήταν ο πρώτος μη κλασματικός αριθμός, εγκαινίασε μια νέα κατηγορία αριθμών, τους «άρρητους».
