Ο Αριθμός του Euler - ΜαθηματιΚά

Μοιραστείτε το!

Εισαγωγή

Στα Μαθηματικά, ένας από τους σπουδαιότερους αριθμούς, με καθοριστική παρουσία σε θεμελιώδη θεωρήματα, είναι ο αριθμός του Euler.

Ο Ελβετός Leonhard Euler (1707 – 1783) υπήρξε ένας απ’ τους περισσότερο παραγωγικούς μαθηματικούς στην ιστορία των Μαθηματικών. Στον Euler οφείλεται ένα σημαντικό μέρος από την ορολογία και το συμβολισμό στα Μαθηματικά, ιδιαίτερα στη Μαθηματική Ανάλυση, όπως πχ. ο συμβολισμός $f(x)$ από τις συναρτήσεις. Επίσης, με τις εργασίες του, συνεισέφερε στη Μηχανική, στη Ρευστοδυναμική, στην Οπτική και στην Αστρονομία.

Ο αριθμός του Euler είναι άρρητος αριθμός, συμβολίζεται διεθνώς με το $e$ και έχει προσεγγιστική τιμή $e\cong 2,718$ . Το συγκεκριμένο σύμβολο – που ο ίδιος ο Euler υιοθέτησε για να τον αναπαραστήσει – , κατά σύμπτωση, είναι το πρώτο γράμμα από το επώνυμο του κορυφαίου μαθηματικού. Θεωρείται ότι η συγκεκριμένη επιλογή οφείλεται στο γεγονός ότι τα προηγούμενα γράμματα, $a,b,c,d$ του αλφαβήτου, ήταν δεσμευμένα καθώς χρησιμοποιούνταν σε διάφορους άλλους τύπους.

Όμως, η πρώτη εμφάνιση αυτού του αριθμού είχε συντελεστεί κάποια χρόνια νωρίτερα.

Το 1683, ένας άλλος μεγάλος Ελβετός Μαθηματικός, ο Jacob Bernoulli (1655 – 1705), στην προσπάθεια εύρεσης της βέλτιστης λύσης ενός προβλήματος ανατοκισμού, ήρθε αντιμέτωπος με τον υπολογισμό της παράστασης,

$\left ( \displaystyle\frac{\nu+1}{\nu} \right )^\nu,$

για “μεγάλες” τιμές του $\nu$ .

Δηλαδή, τρόπον τινά, ο Bernoulli αναμετρήθηκε με το πρόβλημα του υπολογισμού του ορίου,

$\displaystyle\lim_{\nu \rightarrow +\infty}\left ( \frac{\nu+1}{\nu} \right )^\nu.$

Ωστόσο, η εργασία του έμελλε να παραμείνει ανολοκλήρωτη.

Το πρόβλημα ανατοκισμού και ο αριθμός του Euler

Το πρόβλημα που απασχόλησε τον Bernoulli θα μπορούσε να διατυπωθεί ως εξής.

Μία τράπεζα προσφέρει στους πελάτες της το εξής επενδυτικό πρόγραμμα:

Το ποσό που κατατίθεται αποδίδει τόκο $100\%$ στο τέλος του έτους.

Επίσης,

Η απόδοση του τόκου συμβαίνει αναλογικά με τη μεταβολή του χρόνου.

Ποια θα μπορούσε να είναι η βέλτιστη τακτική ανατοκισμού, από πλευράς πελατών, μέσα σ’ ένα έτος, έτσι, ώστε να μεγιστοποιηθεί ο τόκος;

Να αναλογιστείτε, για παράδειγμα, ότι ο πελάτης, διαθέτει ένα αρχικό κεφάλαιο $K_0$ το οποίο επενδύεται ως εξής. Στα μισά του έτους, ο τόκος, ο οποίος θα είναι το $\dfrac{1}{2}$ του αρχικού του κεφαλαίου ( $50\%$ ), επενδύεται στο αρχικό κεφάλαιο $K_0$ . Στη συνέχεια, το επανακεφαλαιοποιημένο ποσό ( $(1+\dfrac{1}{2})K_0$ ) ανατοκίζεται για το υπόλοιπο μισό του έτους. Παρόμοια, στο τέλος του έτους, το συνολικό ποσό θα είναι,

$(1+\dfrac{1}{2})K_0+\dfrac{1}{2}(1+\dfrac{1}{2})K_0=(1+\dfrac{1}{2})^2K_0=(\dfrac{3}{2})^2K_0.$

Μπορείτε να αντιληφθείτε τι θα συνέβαινε αν ο πελάτης εφάρμοζε την προηγούμενη τακτική ανατοκισμού διαιρώντας το διάστημα του έτους σε τρία, τέσσερα, κ.ο.κ., $\nu$ ίσα χρονικά διαστήματα;

Η διαδραστική εφαρμογή

Ο π-e-λάτης έχει πάντα δίκιο!

Στο ακόλουθο πρόβλημα, καλείστε να βοηθήσετε έναν χρηματιστή να διαφυλάξει τα συμφέροντα του πελάτη του. Το πρόβλημα είναι παρόμοιο με το πρόβλημα ανατοκισμού που οδήγησε στην ανακάλυψη του $e$ . Πιθανώς να είναι λίγο πιο ιντριγκαδόρικο ως περισσότερο προσαρμοσμένο στην εποχή μας.

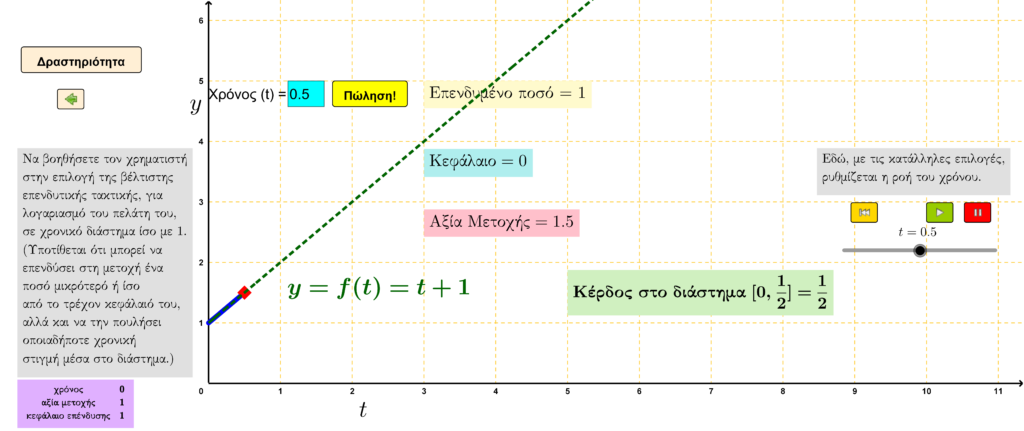
Ένας χρηματιστής, λοιπόν, εκτιμά ότι μια συγκεκριμένη μετοχή μπορεί να ανεβάζει, αναλογικά, με τη μεταβολή του χρόνου, την αξία της, ωσότου, μέσα σε μια συγκεκριμένη χρονική περίοδο, αυξηθεί κατά 100%. Με δεδομένη την εκτίμηση αυτή, ποια θα μπορούσε να είναι η καλύτερη τακτική αγοραπωλησιών από πλευράς του, έτσι, ώστε να μεγιστοποιήσει τα κέρδη του κεφαλαίου ενός πελάτη του ο οποίος θα επενδύσει, αποκλειστικά, στη συγκεκριμένη μετοχή;

Υπόδειξη: Να θεωρήσετε το $1$ ως τιμή για την αρχική αξία της μετοχής και για τη χρονική περίοδο που διαρκεί η αύξησή της σύμφωνα με την εκτίμηση του χρηματιστή. Επίσης, υποτίθεται ότι ο πελάτης μπορεί να επενδύσει στη μετοχή ένα ποσό μικρότερο ή ίσο από το τρέχον κεφάλαιό του αλλά και να την πουλήσει οποιαδήποτε χρονική στιγμή. Ενδεικτικά, να συμπληρώσετε τα κενά του ακόλουθου πίνακα.

ΚΕΦΑΛΑΙΟ ΕΠΕΝΔΥΣΗΣ

(ΣΤΗ ΜΕΤΟΧΗ)

ΧΡΟΝΟΣ

ΚΕΡΔΟΣ

ΤΕΛΙΚΟ ΚΕΦΑΛΑΙΟ

(ΜΕΤΑ ΤΗΝ ΠΩΛΗΣΗ)

Αρχ. Κεφάλαιο ( $K_0$ )

$0-1$

……………………………

που, ίσως, να περιγράφει τις πρώτες σας σκέψεις σχετικά με μια πιθανή επενδυτική τακτική και να προβληματιστείτε, σχετικά, με ενδεχόμενες βελτιώσεις.

Το πρόβλημα παρουσιάζεται και αναλύεται στην παρακάτω διαδραστική εφαρμογή Geogebra. Στόχος της εφαρμογής είναι η ενεργή εμπλοκή σας καθώς οικοδομείται η προσεγγιστική τιμή του αριθμού $e\cong 2,718$ .

Μεταβάλλοντας, κατάλληλα, ορισμένες παραμέτρους του προβλήματος, αναδεικνύονται και οι διάφορες δυνάμεις του $e$ . Έτσι, το πρόβλημα μπορεί να θεωρηθεί ως εφαρμογή της εκθετικής συνάρτησης, με βάση τον αριθμό $e$ .

Καλή ενασχόληση!

Η διαδραστική εφαρμογή για τον αριθμό του Euler

Μία εναλλακτική αναπαράσταση του αριθμού του Euler

Η ισότητα,

$e=\displaystyle\lim_{\nu \rightarrow +\infty}\left (1+\frac{1}{\nu}\right )^\nu,$

με βάση τον διωνυμικό τύπο,

$(\alpha+\beta)^\nu=\sum_{j=0}^{\nu}\left( {\begin{array}{*{20}{c}} \nu \\ j \end{array}} \right){\alpha^j \beta^{\nu-j}},$

όπου $\left( {\begin{array}{*{20}{c}} \nu \\ j \end{array}} \right)=\dfrac{\nu!}{j!(\nu-j)!}$ και $j!=1\cdot2\cdot3\dots\cdot(j-1)j$ , μπορεί να προσφέρει μια πολύ χρήσιμη εναλλακτική αναπαράσταση του $e$ .

Αναλυτικότερα, ο προηγούμενος διωνυμικός τύπος γράφεται ως εξής,

$(\alpha+\beta)^\nu=\alpha^\nu+\nu\alpha^{\nu-1}\beta+\dfrac{\nu(\nu-1)}{2!}\alpha^{\nu-2}\beta^2+\dfrac{\nu(\nu-1)(\nu-2)}{3!}\alpha^{\nu-3}\beta^3\\+\dots+\nu\alpha\beta^{\nu-1}+\beta^\nu,$

οπότε, για $\alpha=1$ και $\beta=\dfrac{1}{\nu}$ ,

$(1+\dfrac{1}{\nu})^\nu=1+\nu\dfrac{1}{\nu}+\dfrac{\nu(\nu-1)}{2!}(\dfrac{1}{\nu})^2+\dfrac{\nu(\nu-1)(\nu-2)}{3!}(\dfrac{1}{\nu})^3+\dots+\nu(\dfrac{1}{\nu})^{\nu-1}+(\dfrac{1}{\nu})^\nu.$

Επομένως,

$(1+\dfrac{1}{\nu})^\nu=1+1+\dfrac{1(1-\dfrac{1}{\nu})}{2!}+\dfrac{1(1-\dfrac{1}{\nu})(1-\dfrac{2}{\nu})}{3!}+\dots+\dfrac{1(1-\dfrac{1}{\nu})(1-\dfrac{2}{\nu})\dots(1-\dfrac{\nu-2}{\nu})}{(\nu-1)!}+\dfrac{1(1-\dfrac{1}{\nu})(1-\dfrac{2}{\nu})\dots(1-\dfrac{\nu-1}{\nu})}{\nu!}.$

Έτσι, για $\nu$ “αρκετά μεγάλα”, φαίνεται ότι καθεμία από τις παραστάσεις,

$1(1-\dfrac{1}{\nu}), 1(1-\dfrac{1}{\nu})(1-\dfrac{2}{\nu}),\dots,1(1-\dfrac{1}{\nu})(1-\dfrac{2}{\nu})\dots(1-\dfrac{\nu-1}{\nu}),$

τείνει να εξισωθεί με το $1$ .

M’ αυτόν τον εμπειρικό τρόπο καταλήγουμε στο συμπέρασμα ότι,

$e=1+1+\dfrac{1}{2!}+\dfrac{1}{3!}+\dots+\dfrac{1}{\kappa!}+\dots,$

το οποίο, όπως θα φανεί, διαδραματίζει καταλυτικό ρόλο στην τεκμηρίωση της αρρητότητας του $e$ .

Η αρρητότητα του αριθμού του Euler

Μπορούμε να αξιοποιήσουμε την προηγούμενη αναπαράσταση για να αποδείξουμε ότι ο αριθμός $e$ είναι άρρητος. Πράγματι, αν υποτεθεί ότι ο $e$ είναι ρητός, δηλαδή αν υποτεθεί ότι $e=\dfrac{\kappa}{\lambda}$ , τότε,

$\dfrac{\kappa}{\lambda}=1+1+\dfrac{1}{2!}+\dfrac{1}{3!}+\dots+\dfrac{1}{\lambda!}+\dfrac{1}{(\lambda+1)!}+\dfrac{1}{(\lambda+2)!}+\dots.$

Έτσι, πολλαπλασιάζοντας τα δύο μέλη της τελευταίας ισότητας με $\lambda!$ , έχουμε,

$\kappa(\lambda-1)!= \lambda!+\lambda!+3\cdot4\cdot\,\dots\,\cdot\lambda+4\cdot5\cdot\,\dots\,\cdot\lambda+\dots+1+\dfrac{1}{\lambda+1}+\dfrac{1}{(\lambda+1)(\lambda+2)}+\dots.$

Από την τελευταία σχέση έπεται ότι $\dfrac{1}{\lambda+1}+\dfrac{1}{(\lambda+1)(\lambda+2)}+\dots\in\math{Z}$ , πράγμα άτοπο.

Η γεωμετρική σύνδεση για τον αριθμό του Euler

Σε αντίθεση με δύο άλλους άρρητους αριθμούς, ορόσημα στην ιστορία των Μαθηματικών, τον αριθμό $\sqrt{2}$ και τον πασίγνωστο $\pi$ , η προέλευση του $e$ δεν είναι καθαρά γεωμετρική. Ωστόσο, ο αριθμός αυτός σχετίζεται έμμεσα με ένα γεωμετρικό πρόβλημα.

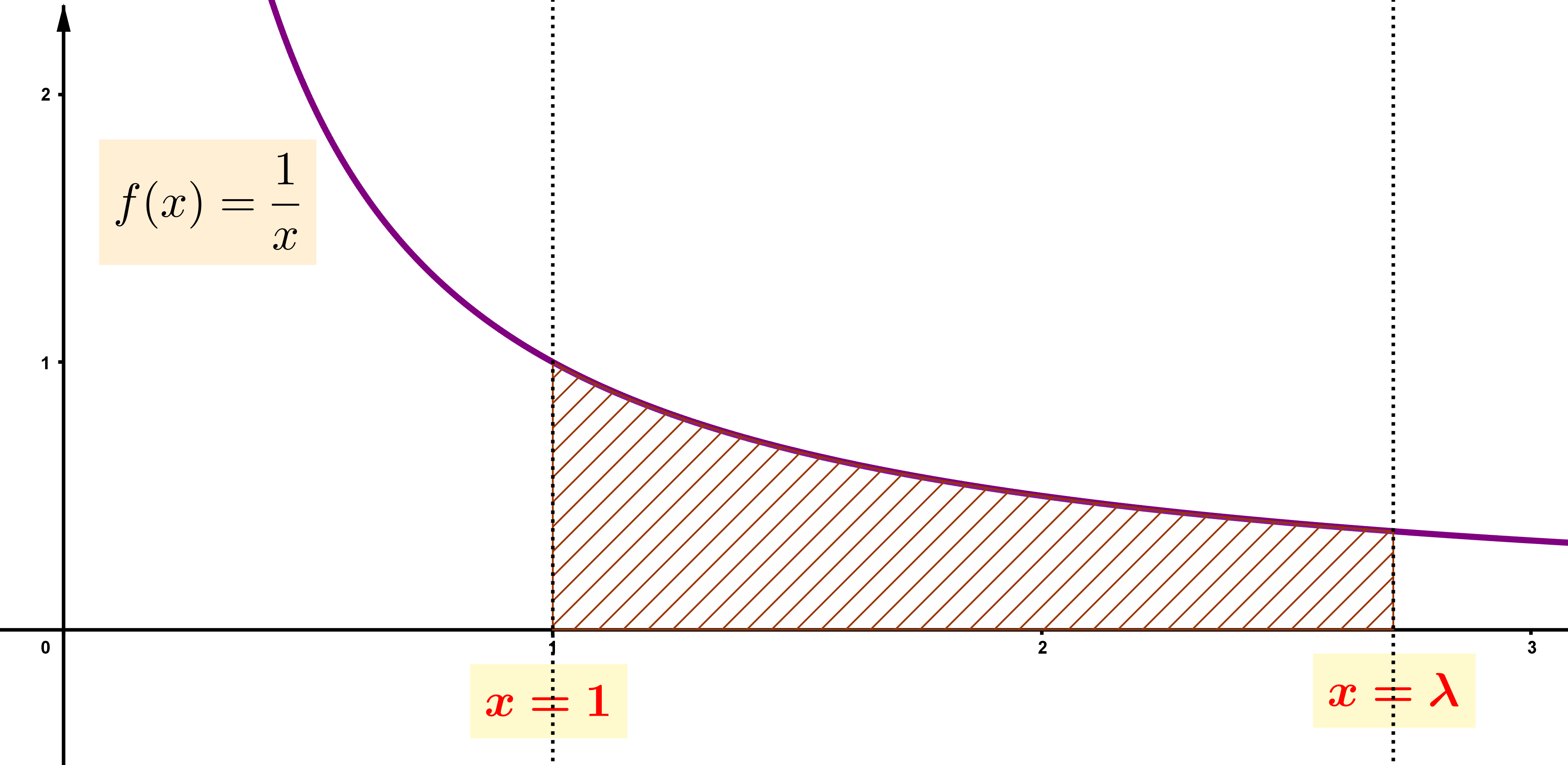
Θα επιχειρήσουμε να εκφράσουμε το εμβαδό, $A$ , του χωρίου που οριοθετείται από το γράφημα της υπερβολής $f(x)=\dfrac{1}{x}$ , τον οριζόντιο άξονα $x'x$ , καθώς και τις κατακόρυφες ευθείες $x=1$ και $x=\lambda$ .

Ο βασικός στόχος είναι το παραπάνω καμπυλόγραμμο χωρίο να προσεγγιστεί από ένα άθροισμα ορθογωνίων των οποίων τα εμβαδά θα μπορούσαν να υπολογιστούν.

Το εγχείρημα είναι γνωστό και ως τετραγωνισμός της υπερβολής.

Ίσως να θυμάστε τη σύνδεση της συνάρτησης, $f$ , με τα αντιστρόφως ανάλογα ποσά. Πράγματι, στον ακόλουθο πίνακα τιμών,

Μέγεθος $\Huge{x}$	$\Large{1}$	$\Large{2}$	$\Large{3}$
Μέγεθος $\Large{y=f(x)}$	$\Large{1}$	$\frac{1}{2}$	$\frac{1}{3}$

ο διπλασιασμός, τριπλασιασμός, κ.ο.κ. της τιμής του μεγέθους $x$ συνεπάγεται τον υποδιπλασιασμό, υποτριπλασιασμό, κ.ο.κ. της τιμής του μεγέθους $y$ και αντίστροφα.

Πώς θα μπορούσε κανείς να εκμεταλλευτεί την προηγούμενη παρατήρηση κατά την αναζήτηση των παραπάνω ορθογωνίων;

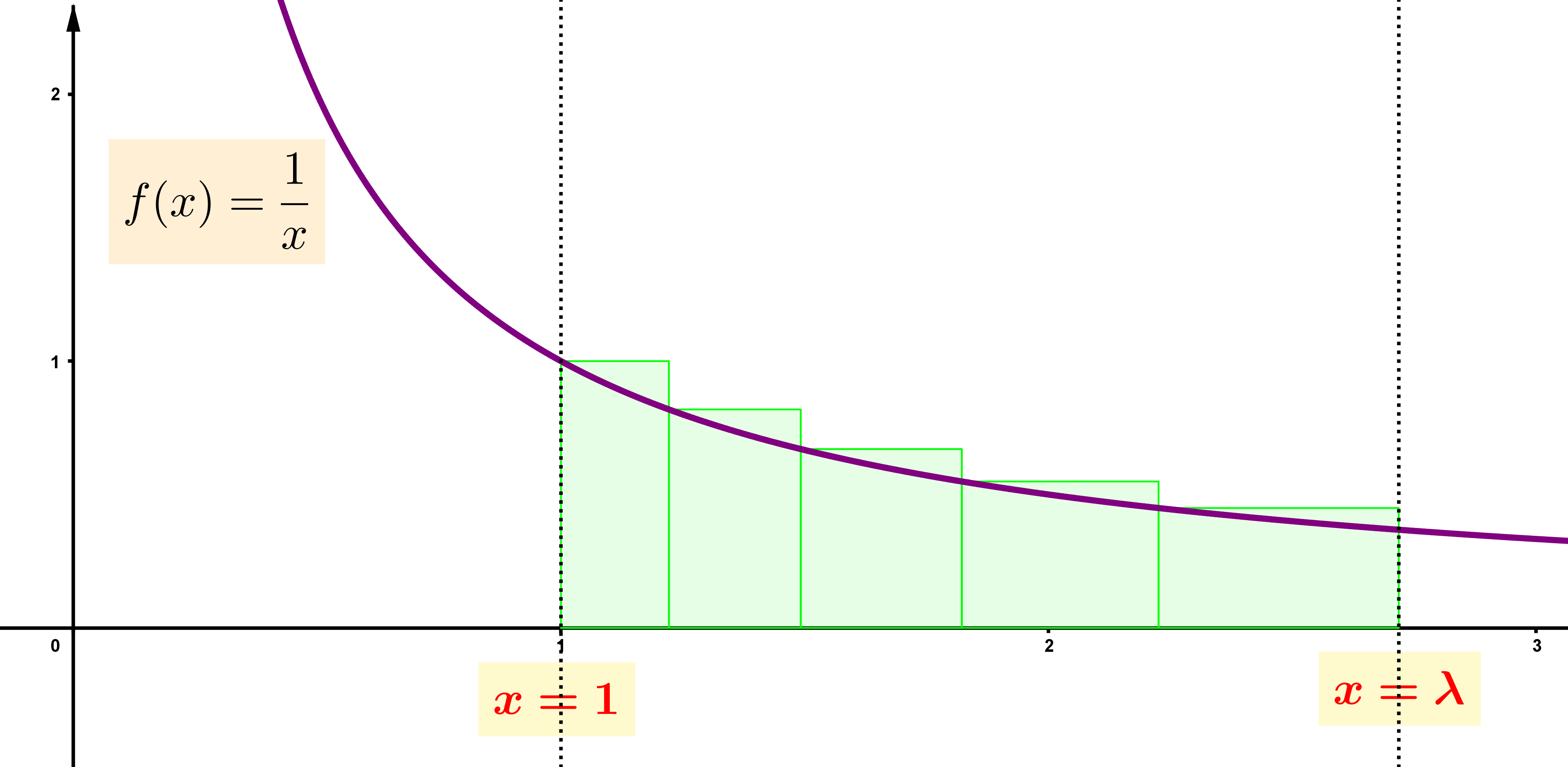
Η επιλογή των ορθογωνίων

1^ο ορθογώνιο: Συμβολίζουμε με τη μεταβλητή $r$ το μήκος της βάσης του στον οριζόντιο άξονα. Αυτό σημαίνει ότι η βάση αυτή οριοθετείται από τους αριθμούς $1$ και $1+r$ του $x'x$ . Το ύψος του επιλέγεται να είναι η τιμή της συνάρτησης, $f$ , στο αριστερό άκρο της βάσης του, δηλαδή $f(1)=1$ . Έτσι, το ορθογώνιο έχει εμβαδό ίσο με $r$ .

2^ο ορθογώνιο: Προφανώς, η βάση του θα τοποθετηθεί, δεξιά, διαδοχικά με τη βάση του πρώτου. Για να είναι η κατασκευή συνεπής προς το προηγούμενο βήμα, θα πρέπει ως ύψος του να θεωρηθεί η τιμή της συνάρτησης στο αριστερό άκρο της βάσης του που, τώρα, είναι το $1+r$ . Οπότε, το ύψος του ισούται με $f(1+r)=\dfrac{1}{1+r}$ .

Τότε, λαμβάνοντας υπόψη τη συζήτηση που προηγήθηκε για τα αντιστρόφως ανάλογα ποσά, είναι εύλογο να επιλεγεί ως δεξί άκρο της βάσης του ορθογωνίου το γινόμενο $(1+r)\cdot(1+r)=(1+r)^2$ . (Το σκεπτικό, επομένως, είναι να πολλαπλασιαστεί το αριστερό άκρο του δεύτερου ορθογωνίου με τον αριθμό με τον οποίο διαιρείται το ύψος του πρώτου ορθογωνίου για να προκύψει το ύψος του δεύτερου ορθογωνίου. Ο αριθμός αυτός δεν είναι άλλος από το $1+r$ . Αυτό έχει ως αποτέλεσμα το ορθογώνιο να είναι ισεμβαδικό με το πρώτο γεγονός που, στη συνέχεια, διευκολύνει κατά τον υπολογισμό του αθροίσματος των εμβαδών τους.)

Η διαδικασία επαναλαμβάνεται πανομοιότυπα για την κατασκευή $\nu$ διαδοχικών ορθογωνίων, όπου η βάση του $\nu$ -οστού καταλήγει να έχει δεξί άκρο το $\lambda$ . (Στην παραπάνω εικόνα, προφανώς, $\nu=5$ .)

Φυσικά, για το $r$ , υπάρχει η δέσμευση που απορρέει από την ισότητα,

$(1+r)^\nu=\lambda.$

Από την άλλη μεριά, αν $S$ δηλώνει το συνολικό εμβαδό των ισεμβαδικών ορθογωνίων, τότε, έπεται ότι $S=\nu\cdot r$ . Συνεπώς,

$(1+r)^S=(1+r)^{\nu\cdot r}=\Big((1+r)^{\nu}\Big)^{r}=\lambda^r.$

Επομένως, $\lambda=\Big((1+r)^{\frac{1}{r}}\Big)^S$ . Ας σημειωθεί ότι για να προσεγγίσει το $S$ το ζητούμενο εμβαδό $A$ , πρέπει το $r$ να είναι όσο το δυνατόν μικρότερο. Για τέτοια, λοιπόν, $r$ , “αρκούντως” μικρά, μπορούμε να θεωρήσουμε ότι,

$\lambda\cong\Big((1+r)^{\dfrac{1}{r}}\Big)^A.$

Ο γεωμετρικός ορισμός

Αναγνωρίζετε τον αριθμό του Euler στην τελευταία σχέση; Αν ναι, τότε, μάλλον θα συμφωνείτε με την ισότητα,

$\lambda=e^A.$

Για $\lambda=e$ , έπεται ότι $A=1$ . Το τελευταίο μας επιτρέπει να αποδώσουμε το εξής κρίσιμο γεωμετρικό χαρακτηριστικό στον αριθμό του Euler:

Είναι εκείνος ο αριθμός, $e$ , ο οποίος καθιστά το εμβαδό του χωρίου, που περικλείεται από το γράφημα της υπερβολής $y=\dfrac{1}{x}$ , τον οριζόντιο άξονα $x'x$ , καθώς και τις κατακόρυφες ευθείες $x=1$ και $x=e$ μοναδιαίο.