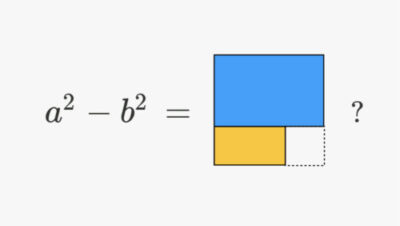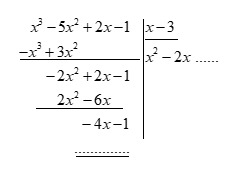Η εξ’ αποστάσεως διδασκαλία έχει τα δικά της κρίσιμα χαρακτηριστικά. Σ’ αυτόν τον τύπο διδασκαλίας, οι διαφοροποιήσεις, οι περιορισμοί και η ιδιαίτερη φύση της επικοινωνίας μεταξύ διδάσκοντα και διδασκόμενου αναπροσαρμόζουν, αναπόφευκτα, το ύφος και τους στόχους του διδακτικού υλικού, σε σχέση με το αντίστοιχο κατά τη διά ζώσης διδασκαλία.
Κατά τη διδασκαλία από απόσταση, το έλλειμα της φυσικής παρουσίας του ίδιου του διδάσκοντα και των διδασκομένων, από αρκετές εκφάνσεις της διαδικασίας, καθιστούν το ρόλο του εκπαιδευτικού ακόμη πιο σύνθετο. Κατά την παραγωγή διδακτικού υλικού, ίσως να πρέπει να συγκεράσει στοιχεία που το καθιστούν ελκυστικό, προνοητικό και προκαταβολικά παρεμβατικό.
Εδώ, θα βρείτε υποστηρικτικό υλικό για να ενισχυθεί η μελέτη διάφορων ενοτήτων. Σε πολλές περιπτώσεις, παρουσιάζονται, προηγουμένως, τα κύρια σημεία της αντίστοιχης θεωρίας τα οποία μπορεί να συνοδεύονται και από διαδραστικές εφαρμογές. Στο τέλος αναπτύσσονται διάφορες ερωτήσεις κατανόησης, ασκήσεις εμπέδωσης αλλά και ασκήσεις απόδειξης. Οι ερωτήσεις – ασκήσεις είναι διάφορων τύπων. Σ’ αυτές περιλαμβάνονται αρκετά θέματα από τη βιβλιοθήκη της αξιολόγησης του κέντρου εκπαιδευτικής έρευνας (Αξιολόγηση των μαθητών του Λυκείου, Τάξεις Α΄,Β΄ και Γ΄, Υπουργείο Εθνικής παιδείας και θρησκευμάτων, ΚΕΕ, Αθήνα 1999).
Οι ερωτήσεις ομαδοποιούνται σε κατάλληλη φόρμα και δημοσιεύονται ως ολιγόλεπτες δοκιμασίες της αντίστοιχης ενότητας. Έτσι, η φόρμα ερωτήσεων θα μπορούσε να αποτελέσει ένα δελτίο εξόδου ολοκληρώνοντας τη μαθησιακή διαδικασία.
Οι απαντήσεις στις φόρμες μπορούν να υποβληθούν ανώνυμα από τον χρήστη καθώς παρέχεται η δυνατότητα ενημέρωσης για την ενδεικτική βαθμολογία του. Χρήσιμη είναι και η δυνατότητα ελέγχου των απαντήσεών του ειδικά όσον αφορά στις ερωτήσεις κλειστού τύπου. Έτσι, αξιολογείται, συγκεντρωτικά, ο βαθμός κατανόησης ενός συγκεκριμένου θέματος.

Εισαγωγή Συχνά, σε διάφορα πλαίσια, από την καθημερινότητα ως τα σχολικά μαθήματα των θετικών επιστημών, αντιμετωπίζουμε καταστάσεις όπου είναι χρήσιμο ...

Εισαγωγή Σην Άλγεβρα της Α΄ Λυκείου, η διερεύνηση της εξίσωσης $x^\nu=\alpha$, όπου $\nu$ φυσικός αριθμός και $\alpha$ πραγματικός αριθμός, ακολουθεί, ...

Εισαγωγή Στην Άλγεβρα της Α΄ Λυκείου, η παραγοντοποίηση ενός τριωνύμου σχετίζεται, έμμεσα, με μια σειρά από άλλες περιοχές του αντικειμένου ...

Εισαγωγή Στην καθημερινότητά μας, σε αρκετές περιπτώσεις, καλούμαστε να υπολογίσουμε ή έστω να εκτιμήσουμε εμβαδά διάφορων βασικών ευθύγραμμων σχημάτων. Για ...

Εισαγωγή Οι σχετικές θέσεις μεταξύ διάφορων γεωμετρικών αντικειμένων, όπως σημείου ως προς κύκλο, ευθείας ως προς κύκλο και κύκλου ως ...

Εισαγωγή Η διάταξη των πραγματικών αριθμών, στην Άλγεβρα της Α' Λυκείου, αποτελεί μια ενότητα με ιδιαίτερη αξία. Άλλωστε, η μελέτη ...

Εισαγωγή Θα μπορούσατε, χαράζοντας δύο τέμνουσες στις παράλληλες γραμμές του τετραδίου σας, να ανακαλύψετε το περίφημο Θεώρημα του Θαλή; Διαβάζοντας ...

Εισαγωγή Η έννοια της συνάρτησης είναι θεμελιώδης και παρούσα σε πολλές πτυχές της καθημερινότητάς μας. Στο Γυμνάσιο, για πρώτη φορά, ...

Εισαγωγή Η γραφική παράσταση μιας συνάρτησης συμπυκνώνει, μ' έναν εύληπτο τρόπο, τα πιο κομβικά χαρακτηριστικά της. Ίσως, να έχετε παρατηρήσει ...

Εισαγωγή Οι γεωμετρικές πρόοδοι αποτελούν έναν ιδιαίτερο τύπο ακολουθιών. Δεν είναι λίγες οι φορές που τέτοιες πρόοδοι ξεπροβάλλουν μέσα από ...

Εισαγωγή Οι αριθμητικές πρόοδοι αποτελούν ειδικές περιπτώσεις ακολουθιών. Συγκεκριμένα, πρόκειται για ακολουθίες αριθμών, όπως η ακολουθία των θετικών άρτιων, $2,4,6,\dots$, ...

Εισαγωγή Μοτίβα Οι ακολουθίες, καθώς και οι δύο ειδικές κατηγορίες τους, οι αριθμητικές και οι γεωμετρικές πρόοδοι, θα μπορούσαν να ...

Εισαγωγή Οι ανισώσεις πρώτου βαθμού εγκαινιάζουν το κεφάλαιο των ανισώσεων στην Άλγεβρα της Α΄ Λυκείου. Με τις ανισώσεις, γενικά, θα ...

Εισαγωγή “Μια εξίσωση δε σημαίνει τίποτε για εμένα εκτός κι αν εκφράζει τις σκέψεις του Θεού.” Σρινιβάσα Ραμάνουτζαν, 1887 – ...

Εισαγωγή Το ορισμένο ολοκλήρωμα είναι ένα ορόσημο σε μια μακρά διαδρομή. Η επιστημονική κοινότητα, παρόλο που τα είχε καταφέρει, περίφημα, ...
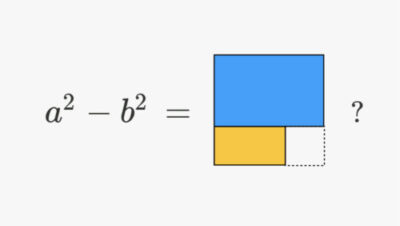
Εισαγωγή Όπως, ίσως, γνωρίζετε από το Γυμνάσιο, οι ταυτότητες είναι εκείνες οι ισότητες οι οποίες περιέχουν μεταβλητές και επαληθεύονται από ...

Εισαγωγή Για τις εξισώσεις δεύτερου βαθμού, η πρώτη, ιστορικά, προσπάθεια επίλυσής τους εδράζεται, γύρω στο 400 π.Χ., στην αρχαία Βαβυλώνα ...
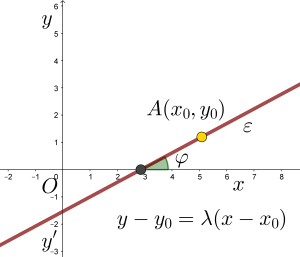
Εισαγωγή Το θέμα της εξίσωσης, για μια ευθεία όπως και άλλων περιπτώσεων γραμμών, π.χ. για την παραβολή, έχει διαπραγματευτεί από ...
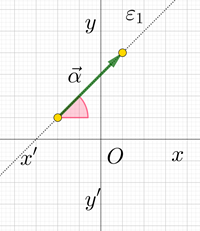
Η ακόλουθη φόρμα, περιλαμβάνει ορισμένες ερωτήσεις κατανόησης και ασκήσεις διαβαθμισμένης δυσκολίας πάνω στον συντελεστή διεύθυνσης διανύσματος. Συντελεστής διεύθυνσης διανύσματος ...
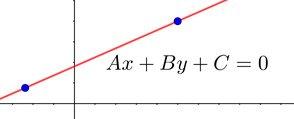
Εισαγωγή Η γενική μορφή εξίσωσης ευθείας είναι ο μαθηματικός τύπος που συγχωνεύει τις δύο διαφορετικές εκδοχές που έχετε διδαχθεί για ...

Εισαγωγή Η διεύθυνση μιας ευθείας, δηλαδή η γωνία που σχηματίζει με τον οριζόντιο άξονα, καθορίζει την κλίση της. Όπως θα ...
Φόρμα ερωτήσεων Στην ακόλουθη φόρμα ερωτήσεων, μπορείτε να ελέγξετε τις γνώσεις σας πάνω στα βασικά σημεία της ενότητας που αναφέρεται ...
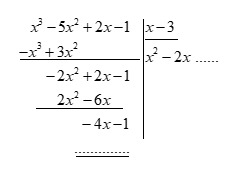
Στην ακόλουθη φόρμα ερωτήσεων, μπορείτε να επεξεργαστείτε μια σειρά από ερωτήσεις κατανόησης και ασκήσεις εμπέδωσης σχετικά με τον αλγόριθμο για ...

Φόρμα ερωτήσεων Στην ακόλουθη φόρμα ερωτήσεων, μπορείτε να επεξεργαστείτε μια σειρά από ερωτήσεις κατανόησης και ασκήσεις εμπέδωσης σχετική με τα ...
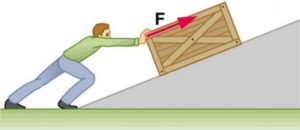
Εισαγωγή Το εσωτερικό γινόμενο διανυσμάτων είναι, αναμφίβολα, μια έννοια με καταβολές από τη Φυσική. Στο μάθημα της Φυσικής, σε σχολικό ...
Φόρμα ερωτήσεων Η ακόλουθη φόρμα ερωτήσεων αναφέρεται πάνω στους τύπους για το μέτρο ενός διανύσματος και για την απόσταση δύο ...
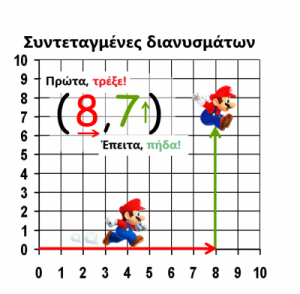
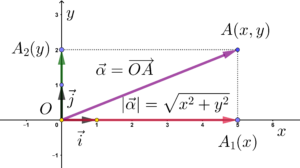
Εισαγωγή Η ενότητα που αναφέρεται στις συντεταγμένες των διανυσμάτων, αποτελεί, για τα Μαθηματικά προσανατολισμού της Β΄ Λυκείου, τον προπομπό της ...
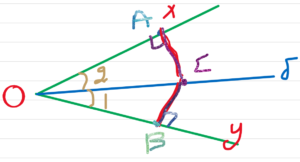
Εισαγωγή Η διχοτόμος γωνίας, ως γεωμετρικός τόπος, παρουσιάζεται, στη Γεωμετρία της Α΄ Λυκείου, ως απόρροια των κριτηρίων ισότητας ορθογώνιων τριγώνων ...

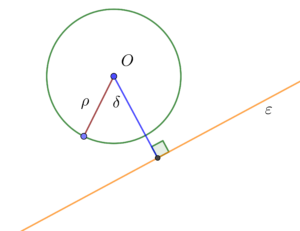
Εισαγωγή Για τα Μαθηματικά Προσανατολισμού της Β΄Λυκείου, ο κύκλος και η εφαπτομένη του, μονοπωλούν - όχι άδικα - σημαντικό μέρος ...

Εισαγωγή Ο τριγωνομετρικός κύκλος αποτελεί θεμέλιο λίθο για τη βάση των κύριων συμπερασμάτων της Τριγωνομετρίας. Ο συγκεκριμένος κύκλος έχει κέντρο ...
Αφόρμηση Μία αρκετά διαδεδομένη διδακτική τάση στα πολυώνυμα, σε σχολικό επίπεδο, είναι μέσω της αναπαράστασής τους ως συναρτήσεων, αξιοποιώντας, ενδεχομένως, ...

Εισαγωγή Η αναγωγή στο πρώτο τεταρτημόριο, που διδάσκεται στην Τριγωνομετρία της Β΄ Λυκείου, αποτελεί μια συνήθη διαδικασία κατά την επεξεργασία ...

Εισαγωγή Στη Γεωμετρία της Α΄ Λυκείου, οι σχετικές θέσεις δύο κύκλων, δηλαδή όλες οι δυνατές περιπτώσεις για τη θέση του ...

Εισαγωγή Στο βιβλίο του, "Math better explained", ο Kalid Azad, χαρακτηρίζει τα ακτίνια του κύκλου ως την "αλτρουιστική επιλογή", σε ...

Εισαγωγή Ένα από τα πιο ενδιαφέροντα και συχνά μελετώμενα θέματα, ειδικά στη Γεωμετρία του Γυμνασίου, είναι οι τρεις κατασκευές για ...